1204 . 樹狀的堆積結構

Submit
Status
Discussion / Solution
Ranklist
Back to Problems List

TopCoder

warner1129

User's AC Ratio

89.3% (50/56)

Submission's AC Ratio

55.6% (79/142)

Tags

TIOJcon 2008-TIOJcon-2nd

Description

還記得puyo疊疊樂(TIOJ-1193) 嗎？

現在我們把滿足puyo疊疊樂性質的二元樹稱為一個「樹狀的堆積結構」：任何非根節點(non-root node)的值都比其父節點(parent node)的數值還要大。

現在給你某棵「樹狀堆積結構」的中序表示法(in-order)，請求出它的前序表示法(pre-order)。

※如果你不知道什麼是中序表示法、前序表示法的話，請參考TIOJ-1108。

Input Format

輸入檔可能包含不超過1000筆測試資料。
每筆測試資料的第一列有一個正整數n(1<=n<=10,000)，代表「堆積樹狀結構」的節點總數。
第二列有n個以空白隔開的正整數，為該「堆積樹狀結構」的中序表示法。
你可以假設同一個樹狀堆積結構裡面，不會有相同的正整數，而且所有數字都不會超過109。
當n=0的時候代表輸入結束。

Output Format

對於每一筆測試資料，請輸出該「堆積樹狀結構」的前序表示法。

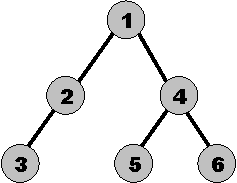
Sample Input 1

6
3 2 1 5 4 6
0

Sample Output 1

1 2 3 4 5 6

Hints

1.這種東西好像又叫做笛卡爾樹(Cartesian Tree)！
2.測試資料當中，99%以上的測試資料的n<=1,000。

※2008/02/02輸入說明修正：感謝math120908。

Problem Source

原TIOJ1204 / TIOJ 2008例行賽02 (prob F)。Problem Setter：Tmt。

Subtasks

No. Testdata Range Score
1 0 100

Testdata and Limits

No. Time Limit (ms) Memory Limit (VSS, KiB) Output Limit (KiB) Subtasks
0 1500 65536 262144 1
Submit
Back to Top