1193 . Puyo疊疊樂
TopCoder
Tags
Description
魔法氣泡似乎歷久彌新,現在又推出了「氣泡疊疊樂」這款不屬於Puyo-Fever當中的小遊戲。
在這款遊戲當中,每一顆泡泡被賦予了一種力量,一旦力量強的泡泡疊在比較弱的泡泡上,就會進入Terrible-Fever狀態,在該狀態底下,此兩泡泡會不斷的互相排斥,不斷的升高、直到塞住其他氣泡的入口為止。
然後你就Game Over了。
不過,很幸運地,你知道每一個泡泡的力量都不一樣,並且這些氣泡疊起來的時候會很自然地形成一棵二元樹(Binary Tree),如圖所示。
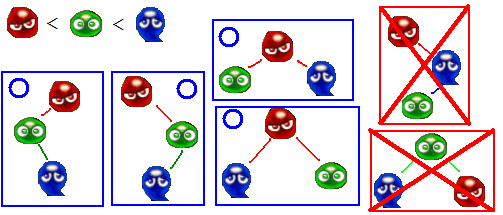
現在請你算算,N顆魔法氣泡,總共有多少種不會進入Terrible-Fever的相異疊法?
只要泡泡疊成的兩種二元樹不太一樣,就是相異的疊法。不必考慮疊起來的泡泡重心穩不穩的問題(即,可以有部分泡泡懸空之類的)。
發明這種有趣而且殺時間遊戲的DarkKnight覺得,如果對於這樣的難題,還得寫大數,好像太對不起大家了。
這樣吧,給你一個數 M,請你計算總方法數除以M的餘數。
Input Format
輸入可能包含多筆測試資料,每筆測試資料佔一列,包含兩個以空白間格的正整數N,M(1<=N<=1,000,000、1<M<231)。若輸入N=M=0請結束程式,不要做任何額外的輸出。測試資料總數不超過1001筆。
※你可以假設M是隨機的數字。
Output Format
對於每筆測試資料請輸出疊泡泡的總方法數N除以M的餘數。
Sample Input 1
1 1000000000 2 1000000000 0 0
Sample Output 1
1 2
Hints
Problem Source
原TIOJ1193 / TIOJ 2008例行賽01-Elite (prob I)。Idea:DarkKnight。
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 100 |
