1157 . 6.線性系統求解
TopCoder
Description
1947年美國勞動統計局花了兩年的時間,收集超過250,000經濟資訊。兩年後哈佛大學Wassily Leontief教授將這些經濟活動分析成500產業,其中包括煤業、汽車業、運輸業等。對每一個產業,Leontief教授用一個線性方程式來表達這個產業如何將其產出分散或影響其他的產業。他的研究開啟了日後利用電腦來解決大型數學問題的先例。Leontief教授後來在1973年獲得諾貝爾經濟貢獻奬。
由於在科學或經濟上所包含的資料都相當多,有很多數學模式都是線性的,所以線性系統求解可以說是相當重要。有關線性系統的解法可以應用高斯消去法(Gauss-Jordan Elimination) 來求解。
假設我們有以下的線性方程組:
<!-- -->
-->
可以用消去法來求解:
步驟一:
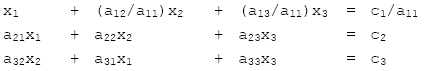
步驟二:
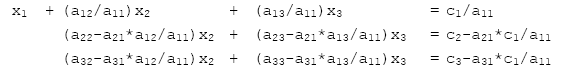
接著再對第二行做步驟一,以此類推。
舉例來說,我們現在來解一個方程組:
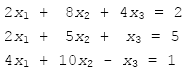
這個方程組可以表示成:
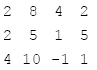
解此方程組的步驟如下:
步驟一:
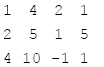
步驟二:
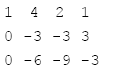
步驟三:
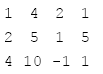
步驟四:
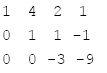
步驟五:
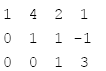
步驟六:
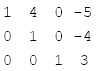
步驟七:
1 0 0 11
0 1 0 -4
0 0 1 3
最後可得解為:
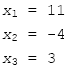
我們接下來討論下面這個方程組:
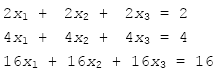
步驟一:
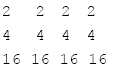
步驟二:
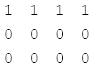
最後可得解為:
無限多組解。
然而在計算的過程中,因為可能使用浮點數的關係,會導致進位誤差以及計算誤差;或者是在不同的計算順序下,也可能會有誤差的產生。如果我們使用分數來表示數字就可以預防浮點數的誤差。我們可以用1/3來表示一個數字,取代原本的0.333333(有遺失精確度的問題)。這麼一來,就可以解決上面所提的錯誤的問題了。
現在請設計一個程式,可以幫我們求解線性系統。注意方程組可能有一組解、無解、或無限多組解。
Input Format
為方便輸入,方程組的變數均省略。第一行是整數n(0<n<50)代表方程組中有n個變數。
接下來會有m行(1≤m≤n),每一行代表一個方程式,若有n個變數,則一行會有n+1個值(例:2 8 4 2代表2x1 + 8x2 + 4x3 = 2),每兩個值之間會有一個或多個空白隔開。方程式中的數字都是整數。
Output Format
第一行為0或1或N分別表示無解、1組解、及無限多組解。若為1組解或無限多組解,請再輸出N行代表一組解,每一行代表一個變數,變數編號從x1, x2, 到 xn(無限多組解時,請只要輸出N即可)。
如果某些變數的解不是整數,請用最簡分數來表示那些解。你可以假設所有數字的分子與分母在運算過程中都不會超過32-bit integer的範圍(但要適時地約分)。如果數字為負的分數p/q,其中p或q其中一個數字為負數,請將分母修正成正數,分子修正成負數。例:-1/3是一個合法的表示法,1/-3則不是。 (輸出解答時,只需在等號前面後面各加一個空白,其他地方不用)
※無限多組解時,只要輸出"N"就好,請不必輸出任一組解~
Sample Input 1
3 2 8 4 2 2 5 1 5 4 10 -1 1
Sample Output 1
1 x1 = 11 x2 = -4 x3 = 3
Sample Input 2
3 1 2 3 0 8 10 12 6 7 8 9 6
Sample Output 2
N
Sample Input 3
3 1 2 3 0 4 5 6 3 7 8 9 0
Sample Output 3
0
Sample Input 4
1 3 10
Sample Output 4
1 x1 = 10/3
Hints
Problem Source
原TIOJ1157 / 93全國賽(prob 6)。
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 20 |
| 2 | 1 | 20 |
| 3 | 2 | 20 |
| 4 | 3 | 20 |
| 5 | 4 | 20 |
