2359 . EZDSA
TopCoder
Tags
Description
//r: 027a872f87c98bf7aead3c514ffb9e5f25719c7d5d4591aa34f3e3388110807d
//s: 4ed20d3dc3265e845fd13c021ca8dce97f2361565e030e5b05d2ccf58dc5357f
//x: 04df4bd35d60b090d6a9da5360479e08fc6fc2b6ece2d5f989735836bb0e508a
//y: 7349916cdf36d4830f752a47ac7ff518bfa8ac92cbad4ad66e9f06e7943deedf
以上是本題的橢圓曲線數位簽章,可以用來證明本題的確是出題者出的(雖然這是廢話)。
什麼?你說你不知道橢圓曲線數位簽章是什麼?
ECDSA (Elliptic Curve Digital Signature Algorithm) 是一種基於橢圓曲線密碼學的數位簽章算法。
在了解什麼是 ECDSA 前,我們要先來簡單了解一下橢圓曲線是怎麼運作的。
模下橢圓曲線 Modular Elliptic Curve
在密碼學中,我們在意的是在模某個質數
給定一個質數
我們說一個點
此外,我們特別定義一個無限遠的點
對於
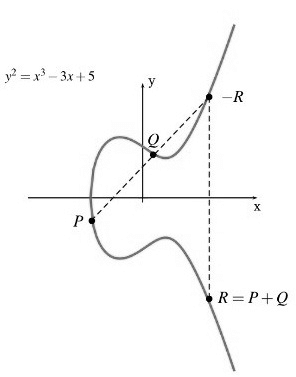
第三點
如果
如果是
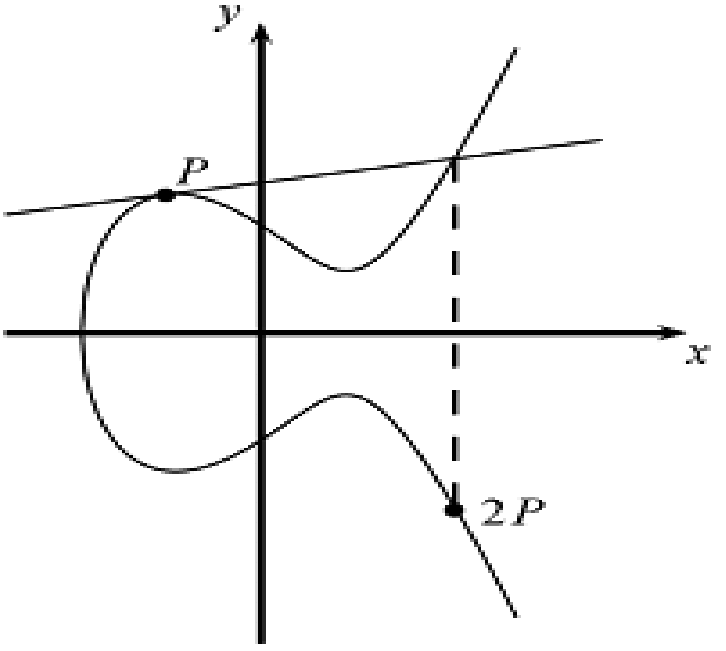
此時以
可以證明
橢圓曲線離散對數問題 Elliptic Curve Discrete Log Problem (ECDLP)
給定一兩的點
這類問題通常很難在合理的時間內解出,除非有特殊的性質(
這也是橢圓曲線數位簽章(ECDSA)的基礎。
橢圓曲線數位簽章算法 Elliptic Curve Digital Signature Algorithm (ECDSA)
數位簽章是一種使用了公鑰密碼學的技術。數位簽章就如同紙本簽章一樣,能被用來確認訊息發送者的身份是否正確,同時使發送者無法否認。
而 ECDSA 則是透過了 ECDLP 的難度來達到難以偽造及難以否認的特點。
更準確來說,ECDSA 需要滿足「正確性」(被正確簽署的簽章總是要被驗證為正確的)和「難以偽造」(沒辦法在合理時間內偽造)兩個性質。
具體來說,假設愛麗絲要用他的私鑰
那麼最常見的實作方式是他們先決定好:
- 一個橢圓曲線
- 算好
- 愛麗絲的公鑰
- 一個雜湊函數
以上的資訊皆可以被公布,不會影響到簽章的安全性及完整性。
接下來,給定一個訊息
- 隨機地抽一個
- 令點
- 如果
特別注意,若
而鮑伯可以由以下步驟驗證簽章
- 檢查
- 令
- 檢查
可以注意到簽章通過檢驗並不百分之百保證是愛麗絲簽的,因為就算
- 私鑰
- 攻擊者沒有花八百輩子的陽壽猜到
在本題實作中,我們考慮以 SHA256 作為
現在,請你實作驗證簽章的演算法,也就是給你
實作細節
secp256k1 的參數如下:(來源:https://en.bitcoin.it/wiki/Secp256k1 )
0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F817980x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B855066263022277343669578718895168534326250603453777594175500187360389116729240326705100207588169780830851305070431844712733806592432759389043357573374824240xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141115792089237316195423570985008687907852837564279074904382605163141518161494337
TIOJ 上的 python 有 SHA256 可以使用。
Input Format
每筆測資有五行輸入。
第一行會輸入以十六進位表示的
第二行會輸入以十六進位表示的
第三行會輸入以十六進位表示的
第四行會輸入以十六進位表示的
第五行會輸入以十六進位表示的
Output Format
如果你判斷簽章是正確的,請輸出 True,否則請輸出 False。
Sample Input 1
d41c263f9e2353fa78fb838a299aee2d1258392d37016230ca8b2154701461f7
bff555b3b919657d3fdedf784f475a551d6f5034de33715b1c43f462a01e6fb4
8ca0f0f5b5c378a20b7c670d754173d1a985ef3495aba4eaf1003c0a46c8c2f2
75771ac5ba51b8fcd810120de8e9131c7a0472d0c2d99ac0b98f762f412f5232
Sample Output 1
Sample Input 2
d41c263f9e2353fa78fb838a299aee2d1258392d37016230ca8b2154701461f7
bff555b3b919657d3fdedf784f475a551d6f5034de33715b1c43f462a01e6fb4
8ca0f0f5b5c378a20b7c670d754173d1a985ef3495aba4eaf1003c0a46c8c2f2
75771ac5ba51b8fcd810120de8e9131c7a0472d0c2d99ac0b98f762f412f5232
Sample Output 2
Hints
- 為什麼是愛麗絲和鮑伯?就只是翻成中文夠奇怪而已。
- 小知識:神祕隨機數的英文 Nonce 同時還有戀同癖、猥褻兒童罪犯的意思。英文真是神祕又隨機啊。
- 目前好像還沒有 Nonce 的公認翻譯,有的話拜託告訴出題者。
Problem Source
TIOJ April Fools Day Contest 2024 pI
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測試資料。 | 0 |
| 2 | 0~3 | 無額外限制。 | 99 |
| 3 | 0~7 | 有額外限制。 | 1 |
