最近 CPVirus 在數學課學到了手算開根號的方法，這個方法大概如下。
為了要做課後練習，現在給你兩個正整數 $A,B$，請你求 $\sqrt[B]{A}$。

以下節錄自范志軒的「開 $n$ 次方根的直式計算與原理」。

若要以直式手算開根號，可以參考以下作法：

1. 首先，由小數點位置開始向左或向右每二位數標上一撇，由左至右，分成 $n$ 小節。622521 為例，共可分成三小節，而每一小節恰可計算出平方根的一位數字，如 62'25'21。
2. 由第一小節開始，估算出正整數 $a$ ，使得 $a^2$ 最接近此節的數字。將第一小節的數減去 $a^2$，連同次一小節的數字下降至下一列。例如取 $a=7$，則有
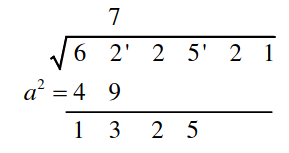
3. 令 $10a=a_1$，估算求出正整數 $b$ ，使得 $2a+b$ 乘以 $b$ 最接近此列上的數。用此列上的數減去 $(2a_1+b)\times b$ ，再連同次一小節的數字下降至下一列。
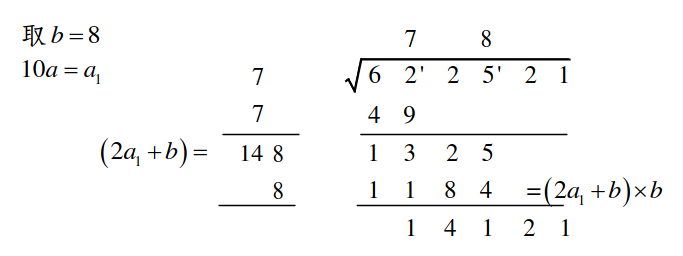
4. 重複以上步驟直到降下的數字為 $0$ 所得即為所求。

（更詳細的方法請參考上列連結）

不難可以發現，在進行直式開根號的時候，我們運用到了二項式的展開，即 $(a+b{)}^2=a^2+2ab+b^2$。

在開三次、甚至 $n$ 次根號的算法中，我們也可以依此類推。雖然此方法以人工進行直式運算顯然不切實際，甚至不如採用十分逼近法恰當，然而在求次方根的過程中，同學仍可觀察到規律變化的優美性質，若是具有程式設計能力的同學，可嘗試設計開 $n$ 次方根的演算法，這會是一個不錯的練習。但在現實生活中，我們也不用算的那麼精確，只要輸出的絕對或相對誤差在 $1^{0-9}$ 以內就可以了。

對了，如果你有好好修數學課的話，你也可以試試看寫牛頓法，搭配 NTT 等算法進行多項式及大數的微分、除法等操作進行運算喔。若想測試大數乘法的模板，可以上 Library Checker 或試試看 1064 喔。