2219 . 長頸鹿園
TopCoder
Tags
Description
附中附近有一個長頸鹿園新開幕，長頸鹿園有 $N$ 個區域，並且有 $N-1$ 條走道連接它們，每條走道都會連接兩個區域，並且從任何一個區域開始，都能沿著走道走到其他任何一個區域。
為了讓遊客在接下來 $N$ 天每天都有新鮮感，園方決定逐步開放園區：在第一天，只有第 $1$ 個區域是開放的，接下來在第 $i$ 天，會多開放第 $i$ 個區域，也就是說，在第 $i$ 天時，只有第 $1$ 到 $i$ 個區域是開放的，其他區域都禁止進入。而且如果一條走道連接的兩個區域，有至少一個不開放，那麼這條走道也不會開放。保證從一個開放的區域走到另一個開放的區域時，不需要經過未開放的區域。
長頸鹿園很特別，每個區域都有設置出入口，遊客可以選擇在任何一個區域進入或離開長頸鹿園。熱愛長頸鹿的校長決定在接下來 $N$ 天內，每天都造訪長頸鹿園，不過他會有以下這些限制：
- 一但離開長頸鹿園，這天就不能再進入長頸鹿園。
- 在離開一個區域後，當天不能再回到同一個區域。
如果違反這些限制，就會在黑特附中被批評校長整天都在逛長頸鹿園。雖然校長不希望看到這樣的貼文，但他仍然非常熱愛長頸鹿，因此他每天都想要造訪盡量多個區域。
為了避免選擇障礙，校長想要知道，在符合限制和他的要求的情況下，每一天他有幾種方式選擇要造訪的區域集合。
測資限制
- $1 \leq N \leq 10^ 5$
- $p_i < i$
Input Format
第一行有一個整數 $N$，表示長頸鹿園的區域數量。
第二行有 $N-1$ 個整數 $p_2,p_3,\dots,p_N$，其中 $p_i$ 表示有一條走道連接第 $p_i$ 和第 $i$ 個區域。
Output Format
輸出 $N$ 行，其中第 $i$ 行輸出一個整數，表示在第 $i$ 天，校長有幾種方式選擇要造訪的區域集合。
Sample Input 1
9
1 1 1 4 4 4 1 2
1 1 1 4 4 4 1 2
Sample Output 1
1
1
1
3
2
4
6
9
3
1
1
3
2
4
6
9
3
Hints
長頸鹿園的地圖如下圖所示：
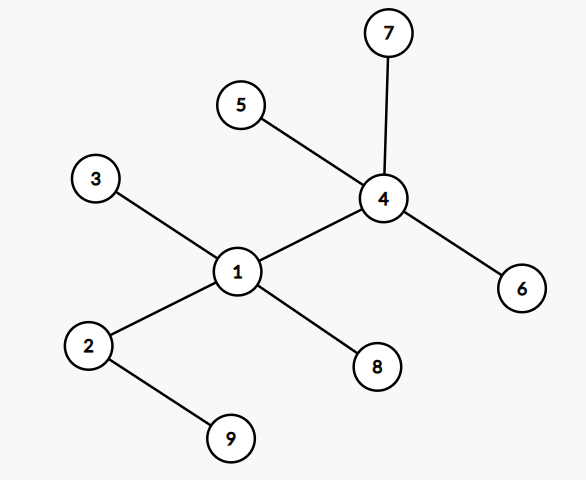
在第 4 天時，校長可以選擇的要造訪的區域集合有：
- $\{2,1,3\}$
- $\{3,1,4\}$
- $\{4,1,2\}$
在第 9 天時，校長可以選擇的要造訪的區域集合有：
- $\{9,2,1,4,7\}$
- $\{9,2,1,4,6\}$
- $\{9,2,1,4,5\}$
Problem Source
2021 師大附中校隊培訓 模擬競賽
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0 | 範例測資 | 0 |
| 2 | 0~10 | $N \le 500$ | 13 |
| 3 | 11~16 | 除了第 $1$ 個區域，每個區域最多只連接兩條走道 | 21 |
| 4 | 0~10, 17~28 | $N \le 5000$ | 25 |
| 5 | 0~38 | 無額外限制 | 41 |