2172 . 物種演化 (Evolution)
TopCoder
Description
演化論是近代生物學中一個重要的學說，用來解釋生物在各世代之間存在差異的現象。透過各種演化證據，生物學家們能夠推斷兩物種間的親緣關係，並基於此資訊建立一個樹狀結構，來展現一個可能的演化過程。
小美在生物課聽到老師介紹演化樹時，覺得非常有趣，回家後立刻上網查了一些演化樹的例子（如下示意圖）。
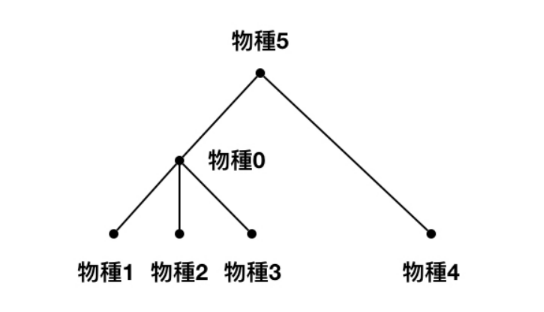
小美看著查到的資料，突發奇想：假設演化樹上的每個節點都代表一個物種，兩節點間在演化樹上的「路徑長度」愈短，是否就顯示兩物種的親緣關係愈相近呢？（此處的路徑長度指的是演化樹上兩點間路徑上的邊個數）小美興沖沖的去和老師討論這個想法，老師的回覆是「不全然正確」。然而小美覺得她的想法頗有可取之處，還是想看看她這個觀察正確性有多高。於是小美委請一位會寫程式的同學大美，幫助她從演化樹中搜集一些她需要的資料。
大美接到的任務如下：給定一個 $n$ 個點的演化樹，每個點代表一個物種，以及 $m$ 個物種的配對，請計算每對物種之間的路徑長度。注意，因為小美給資料時給的很隨興，$m$ 個物種配對中可能有很多重覆。
Input Format
每一筆測試資料包含 $n+m$ 行，其中第一行為正整數 $n$ 與 $m$，物種編號由 $0$ 至 $n-1$。接下來 $n-1$ 行每行有 $2$ 個整數 $i$ 與 $j$，表示物種 $i$ 和物種 $j$ 在演化樹上有邊相連。接下來 $m$ 行，每行有兩個整數 表示欲探討的物種對 $x$ 與 $y$。同一行的二整數以一空白分隔。其中 $n\leq 10^ 5, m\leq 2.5\times10^ 6$。
Output Format
輸出有 $m$ 行，每行一個整數，依序為兩物種在演化樹上的路徑長度。
Sample Input 1
2 9
3 9
7 9
8 5
9 5
6 1
0 1
5 4
1 4
2 3
8 6
1 7
9 5
5 0
Sample Output 1
4
4
1
3
Sample Input 2
1 0
0 2
0 3
1 0
0 2
2 3
1 2
2 1
Sample Output 2
1
2
2
2
Hints
本題共有四組測試資料，每組可有多筆測試資料：
第一組測試資料：$n\leq 500, m\leq 7\times10^ 5$，共 23 分；
第二組測試資料：$n\leq 2000,m\leq 2000$，共 32 分；
第三組測試資料：$n\leq 1.5\times10^ 4, m\leq 10^ 6$，共 26 分；
第四組測試資料：無其他限制，共 19 分。
Problem Source
108 北市賽 pD
testdata set by Omelet
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~9 | $n\leq 500, m\leq 7\times10^ 5$ | 23 |
| 2 | 10~14 | $n\leq 2000,m\leq 2000$ | 32 |
| 3 | 10~19 | $n\leq 1.5\times10^ 4, m\leq 10^ 6$ | 26 |
| 4 | 0~34 | 無其他限制 | 19 |