2170 . 地圖編修 (Map)

Submit
Status
Discussion / Solution
Ranklist
Back to Problems List

TopCoder

腦子裝咖哩
想像不出自己 AC 的題目是實作不出來的！雖然想像得出來也不一定可以就是了

User's AC Ratio

94.7% (90/95)

Submission's AC Ratio

30.0% (185/617)

Tags

北市賽 2019-北市賽

Description

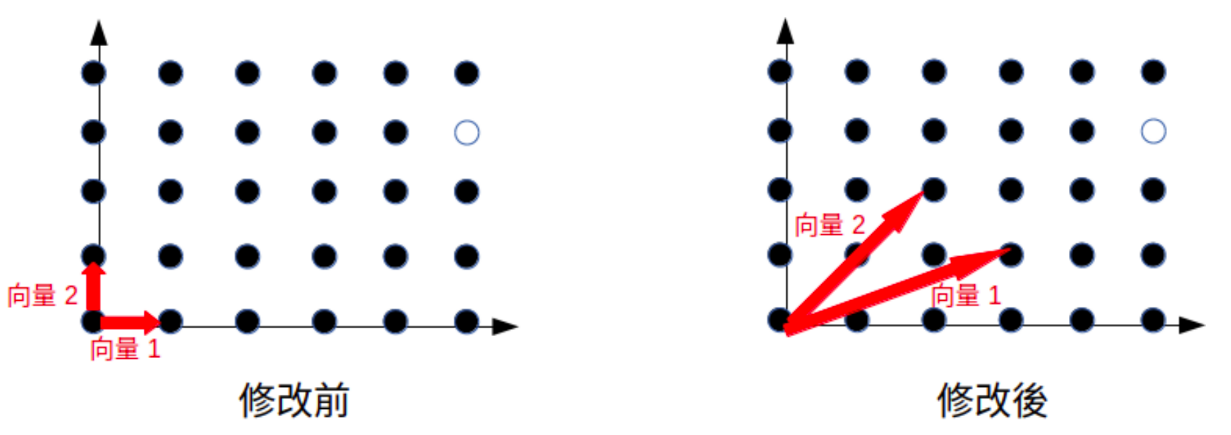
在這世界上有一種外星人，跟活在三度空間的地球人不一樣，他們是活在N 維的空間中，所以想當然，這種外星人的地圖也是透過 N 維的單位向量來表示特定位置的座標。有一天，外星人的皇帝突發奇想，覺得透過單位向量來作為地圖的依據太無聊了，他決定重新定義所謂的「座標軸」，並且座標軸之間也不一定需要是正交的關係。

以上圖為例，這是一個二維的座標圖，空白的點代表外星人皇宮的位置。在原先的座標軸中，外星人皇宮的位置可以用座標[5, 3]來表示，因為該點的位置可以用5個向量1和3個向量2來表示。在皇帝修改座標軸之後，雖然外星人皇宮的位置沒有改變，但座標卻改成 [1, 1]，因為該位置可以用1個向量1和1個向量2來表示。

要注意的是，每個維度都是環形的概念，也就是座標的範圍都在 0 到 M−1 之間，超過的部分會回到 0 後再繼續前進。同時，因為外星人不喜歡小數點，因此所有的座標都是整數。相關的例子可以參考範例測資。請寫一個程式來幫忙進行座標的轉換。

Input Format

第一列有兩個正整數 N,M，其中 N 代表維度的個數， 0<N≤M， M 必為質數且最大為 65537。第二列則是有 N 個數字，代表在原始座標軸皇宮的座標位置。接下來 N 列則是代表皇帝所決定的座標軸的向量，每一列都有 N 個數字，數字大小介於 0 到 1000，但若 M≤1000，則介於 0 到 M−1。

Output Format

請輸出給定的原始座標在新的座標軸底下的座標位置。(測資保證唯一解。)

Sample Input 1

//(題目敘述)
2 101
5 3
3 1
2 2

Sample Output 1

1 1

Sample Input 2

2 101
10 11
3 2
4 7

Sample Output 2

2 1

Sample Input 3

3 101
69 59 89
5 4 2
3 6 7
2 0 1

Sample Output 3

10 20 30

Hints

範例 1 說明：
1*[3 1] + 1*[2 2]
=[5 3]

範測 2 說明：
2*[3 2] + 1*[4 7]
=[10 11]

範測 3 說明：
10*[5 4 2] + 20 *[3 6 7] + 30 *[2 0 1]
= [170 160 190] 對 101 取餘數
= [69 59 89]

本題共有三組測試資料：
第一組測試資料，N=2，共 17 分；
第二組測試資料，N=3，共 27 分；
第三組測試資料，N≤100，共 56 分。

Problem Source

108 北市賽 pB
testdata set by Omelet

10/29 更新subtask測資&rejudge

Subtasks

No. Testdata Range Constraints Score
1 0~4 N=2 17
2 5~9 N=3 27
3 0~24 N≤100 56

Testdata and Limits

No. Time Limit (ms) Memory Limit (VSS, KiB) Output Limit (KiB) Subtasks
0 3000 262144 65536 1 3
1 3000 262144 65536 1 3
2 3000 262144 65536 1 3
3 3000 262144 65536 1 3
4 3000 262144 65536 1 3
5 3000 262144 65536 2 3
6 3000 262144 65536 2 3
7 3000 262144 65536 2 3
8 3000 262144 65536 2 3
9 3000 262144 65536 2 3
10 3000 262144 65536 3
11 3000 262144 65536 3
12 3000 262144 65536 3
13 3000 262144 65536 3
14 3000 262144 65536 3
15 3000 262144 65536 3
16 3000 262144 65536 3
17 3000 262144 65536 3
18 3000 262144 65536 3
19 3000 262144 65536 3
20 3000 262144 65536 3
21 3000 262144 65536 3
22 3000 262144 65536 3
23 3000 262144 65536 3
24 3000 262144 65536 3
Submit
Back to Top