你聽說過小向的故事嗎？

傳說中，小向是個有著強大法力的人，尤其是他的獨創神技「轉眼皮」更是名聞遐邇。「轉眼皮」的神技更幫助他贏得了數次 IMO（宇宙際魔法奧林匹亞，Inter-universal Magic Olympiad）的獎牌。秉持著精益求精的精神，雖然這世界上還沒有已知能克制「轉眼皮」的人或技能，小向仍然固定研究著各種與「轉」有關的魔法與知識，以讓他的轉眼皮能力更強、更難破解。

近期小向恰好研究到了一種特殊的魔法陣。這種魔法陣的形狀非常簡單，就是由許多個正三角形疊成一個大的正三角形，而每個小三角形的頂點都有編號，編號的規則是由左到右、再由上到下從0開始用連續的整數編號，直到每個頂點都被編號，如下圖所示。

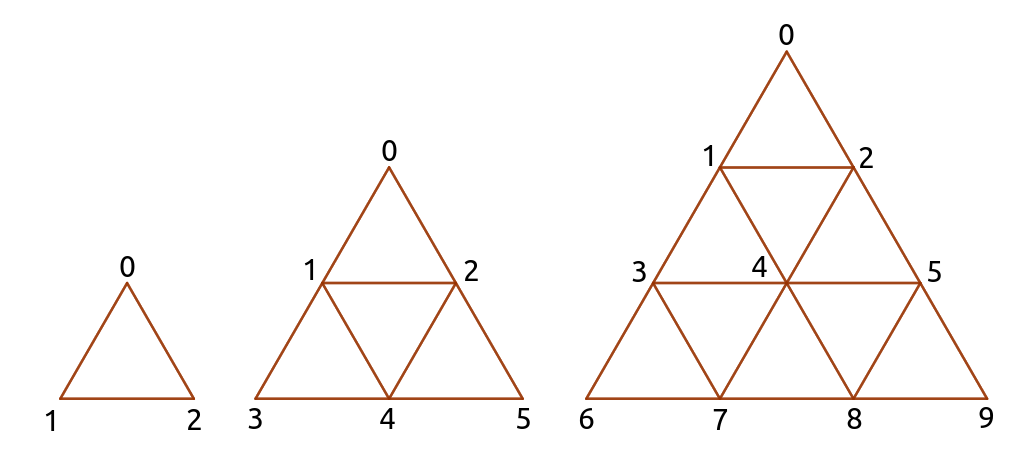
這個魔法陣可以用各種不同的規模（術語稱為「魔階」）出現，而魔階的大小可以從這個魔法陣疊了幾層的小三角形得知。例如上圖的三個魔法陣，由左到右的魔階分別是 1、2、3。可想而知，「魔階」愈高的魔法陣的法術效果愈強，但是也愈難操縱。

至於這個魔法陣為什麼與「轉」有關呢？原來，要透過這個魔法陣施法，必須要先啟動這個魔法陣。而啟動的方法與「轉」的技術密切相關：施法者必須手持魔杖，從大三角形最上面那個點（也就是頂點0）開始，沿著這個魔法陣上的邊描繪整個魔法陣。描繪的過程中，魔杖不能離開魔法陣，且每個三角形的每條邊都只能恰好經過一次（不能完全不經過、也不能經過兩次或以上），否則將無法成功啟動魔法陣。

這個描繪的過程雖說起來容易，但實際上大有學問。在描繪的過程中，魔杖與魔法陣的交互作用會使得魔杖帶有強大的魔法慣性，要使魔杖描繪出魔法陣上的轉角，必須透過「轉」的法術才能使魔杖改變前進的方向。而「轉」同時也是使魔法陣帶有魔力的關鍵因素：在施法者使用「轉」的時候，一部分「轉」的魔力會被儲存在魔杖轉向的地方，作為最終啟動魔法陣時的魔法能量。

眼皮身為追求強大法力的人，再加上他對「轉」法術的嫻熟，他決定要把盡可能多的魔力儲存在魔法陣中。因此，他希望魔杖每經過一個頂點就要使用一次「轉」。由於使用「轉」法術後魔杖必須轉向（否則魔杖很有可能會損壞），所以在施法前必須要仔細規劃好描繪的路徑，以避免魔法陣啟動失敗。

以魔階為2的魔法陣舉例，如果讓魔杖依序經過頂點 0、1、4、5、2、4、3、1、2、0，這樣每經過一個頂點都有使用一次「轉」。但是如果是依序經過頂點 0、1、4、2、5、4、3、1、2、0，在第二次經過頂點4的時候就不能使用「轉」，雖然可以啟動魔法陣，但仍然不符合眼皮的要求。

你，身為眼皮的魔法助手，決定幫助眼皮規劃一個符合他要求的魔法陣描繪路徑。然而，由於眼皮的魔法陣魔階實在是太高了，所以你決定寫一個程式把路徑算出來再提供給眼皮參考。