1876 . 回家
TopCoder
Tags
Description
你解開了櫻的魔法。(詳情請見TOIJ 1875)
你，妹可，今天也努力的想變成溫拿。
「櫻感到很抱歉，喔膩醬...」魔法被破解之後，櫻低著頭啜泣。
「難怪我覺得怪怪得，原來是妳。」
「嗚...嗚...」
「喔膩醬！你不要對她那麼壞，這樣你會沒辦法變成溫拿喔！」夏梨指著你說。
「哎...那我應該怎麼辦...」
「去向櫻道歉啊。」夏梨用一付理所當然的表情對你說。
「疑？！為甚麼是我要道歉！？」
「喔膩醬...之前的帳我還沒跟你算呢...」
「好好好...對不起我錯了，我去就是了嘛...」
到完歉之後...
「我們兩個以後就一起跟著喔膩醬吧！」夏梨對櫻說。
「嗯！❤」
「我們兩個都不可以偷偷的一個人跟喔膩醬玩喔！」她們兩個達成了協議。
可是你馬上就想到問題了，以夏梨和櫻的個性，假設夏梨跟櫻同時在你家裡，那麼你要在和其中一個人獨處被另外一個人知到，那一定會出BUG！！（可能會被這樣）
因為你家是個簡單多邊形，就算夏梨和櫻同時在家裡，兩人之間還是有可能互相看不見的，為了避免上面的情況發生，你想要寫個程式來計算現在和其中一個人OOXX是不是安全的。
我們說現在是安全的，代表你不會和其中一人獨處，也就是你和其中一人OOXX時，另外一個人可以看的見。
Input Format
第一行給定多邊形之邊數量 $N (3 \le N\leq1000000)$，代表你家的牆壁數量。
第二到 第$N+1$行 給定多邊形各點（保證多邊形不自交）
第$N+2$行給定兩組點座標（$A_x, A_y, B_x, B_y$），分別代表夏梨和櫻當時的位置。
題目中所有數值皆可以用$int32$資料型態存儲
Output Format
你可以相信夏梨在位置$A$，櫻在位置$B$，
若$A, B$都不在家裡，則輸出"ERROR!"（不含引號）
若僅$A$不在家裡，則輸出"A troll!"
若僅$B$不在家裡，則輸出"B troll!"
若$A,B$都在家裡，且$A$可以看到$B$($\overline{AB}$之間無障礙物)，則輸出"Okay!"
若$A,B$皆多邊形內，且$A$無法看到$B$($\overline{AB}$之間有障礙物)，則輸出"Bug!"
（若只是多邊形端點在$\overline{AB}$上，則視為無障礙物！）
（判斷障礙物時，不判斷第$N$個點到第$1$個點那條邊。）
Sample Input 1
0 0
5 10
10 0
5 5
3 4 7 4
Sample Output 1
Sample Input 2
0 0
5 10
10 0
5 5
3 4 4 6
Sample Output 2
Sample Input 3
0 0
5 10
10 0
5 5
4 5 6 5
Sample Output 3
Sample Input 4
0 0
5 10
10 0
5 5
4 6 0 4
Sample Output 4
Hints
（下圖皆未按比例繪製）
對於Sample 1的狀況：
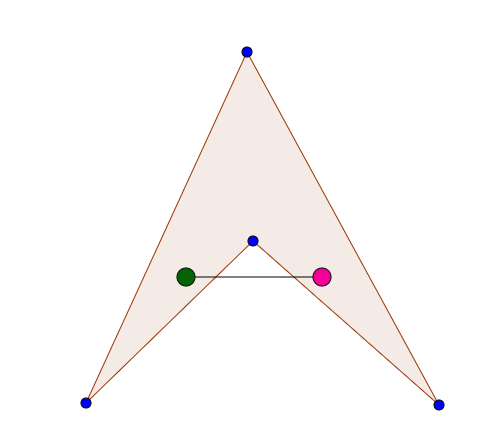
對於Sample 2的狀況：
對於Sample 3的狀況：
對於Sample 4的狀況：
話說後來，
「喔膩醬！！！你和櫻在做甚麼！！！」
「喔膩醬只是在和我玩醫生遊戲而已啊。」
「喔膩醬只能跟我玩！！」
「夏梨快去幫喔膩醬準備午餐吧，喔膩醬繼續幫櫻看病吧~~」
「嗚.....喔！膩！醬！」
看來你的程式一點都沒有用。
Problem Source
2015年建中校內培訓第七次模擬賽
2018/09/14 測資修正by Yihda Yol
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0~1 | 10 |
| 2 | 2~5 | 20 |
| 3 | 6~11 | 30 |
| 4 | 12~15 | 10 |
| 5 | 16~19 | 30 |