1842 . [IOI 2013] 王八 Wombats
TopCoder
Tags
Description
布里斯本現在已經被大量突變的袋熊(wombat)佔領,而你必須帶領人們到安全的地方。
布里斯本的道路是以大型網格(grid)的形式呈現。有R條東西向的水平道路,由北到南依序標示為0, ... ,(R – 1);另外有 C 條南北向的垂直道路,由西到東依序標示為 0, ... , (C – 1),如下圖所示。
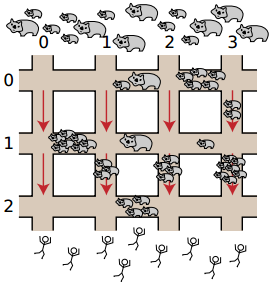
袋熊(wombat)由北方入侵,而人類則逃往南方。人類在水平方向的道路可以往東或往西逃跑,但是在垂直方向的道路只能往南方,也就是安全的地方前進。
水平道路 P 與垂直道路 Q 的交會處以 (P, Q) 表示。兩個交會處之間的道路區段(segment)會包含某數量的袋熊(wombat),這個數量會隨著時間而改變。你的任務是引導每個人從最北方(水平道路 0)的某個給定交會處,到達最南方(水平道路R – 1)的某個給定交會處,使他們行經的路線盡可能遇到最少數量的袋熊(wombat)。
一開始會給定網格的大小以及每個道路區段的袋熊(wombat)數量。接著你將會被給予一連串共E個事件,每個事件可能是:
改變(change),會更改某個道路區段的袋熊(wombat)數量。
逃跑(escape),也就是某個人出現在水平道路0 的某個已給定交會處,而你必須找出一條路線到達水平道路 R – 1 的一個已給定交會處,使得途中盡可能遇到最少數量的袋熊(wombat)。
Input Format
第一行有兩個以空白隔開的正整數R C,表示水平道路數與垂直道路數。
第二行開始有R行,每行為H[i][0] ... H[i][C – 2],其中H[P][Q]給定介於交會處(P, Q)與(P, Q + 1)的水平道路區段所包含的袋熊(wombat)數量。若C = 1,不需要空白數行(第2行到第R + 1行)來表示在水平道路上的袋熊(wombat)數量。
接下來有R-1行,每行為V[0][0] ... V[0][C – 1],其中V[P][Q]給定介於交會處(P, Q)與(P + 1, Q)的垂直道路區段所包含的袋熊(wombat)數量。
接著是一個數字E,表示事件總數。
然後是E行事件的敘述,依照事件發生的順序,每個事件一行:
1 P Q W,表示介於交會處(P, Q)與(P, Q + 1)之間的水平道路區段的袋熊(wombat)數量變更為W。
2 P Q W,表示介於交會處(P, Q)與(P + 1, Q)之間的垂直道路區段的袋熊(wombat)數量變更為W。
3 V1 V2,要你輸出計算當一個人由交會處 (0, V1) 行進到 (R – 1, V2) 時,至少一定會遇到的袋熊(wombat)數量。
對於第一種事件的限制:
P:指出哪個水平道路被影響(0 ≤ P ≤ R – 1)。
Q:指出區段位於哪兩個垂直道路之間(0 ≤ Q ≤ C – 2)。
對於第二種事件的限制:
P:指出哪個水平道路被影響(0 ≤ P ≤ R – 2)。
Q:指出區段位於哪兩個垂直道路之間(0 ≤ Q ≤ C – 1)。
對於第三種事件的限制:
V1:指出這個人從水平道路 0 的哪個地方開始出現(0 ≤ V1 ≤ C – 1)。
V2:指出這個人最後出現在水平道路 (R – 1) 的哪個地方(0 ≤ V2 ≤ C –1)。
輸入限制:
對於9%的測資滿足,C = 1。
對於12%的測資滿足,R, C ≤ 20,且不會有改變的事件。
對於16%的測資滿足,R, C≤ 100, 並且最多有 100 次 escape。
對於18的測資滿足,C = 2。
對於21%的測資滿足,C ≤ 100。
對於24%的測資滿足,2 ≤ R ≤ 5,000,1 ≤ C≤ 200,最多500次改變(事件1與事件2的總數),最多200,000 次 escape(事件3的總數)。
在任何時間在任何區段最多 1,000 隻袋熊(wombat)
Output Format
對於每個逃跑事件(即第三種事件),輸出一個數字於一行表示每次逃跑至少需要遇到多少袋熊(wombat)。
Sample Input 1
3 4 0 2 5 7 1 1 0 4 0 0 0 0 2 0 3 4 7 5 3 2 1 3 3 3 2 0 0 5 1 1 1 6 3 2 1
Sample Output 1
2 7 5
Hints

上圖顯示水平道路數量R = 3 以及垂直道路數量 C = 4 的一個初始地圖,每個道路區段皆標示了該區段的袋熊數量。考量以下的連續事件:
一個人出現在交會處A = (0, 2),並且希望逃到交會處 B = (2, 1)。她遇到的袋熊數量最少可以是 2,如虛線所示。
另一個人出現在交會處 X = (0, 3),並且希望逃到交會處Y = (2, 3)。他遇到的袋熊數量最少可以是 7,同樣如虛線所示。
兩個改變的事件產生:垂直道路 0 最頂端區段的袋熊數量更改為 5,而水平道路1 中間區段的袋熊數量更改為 6,詳見下圖圈起來的數字。
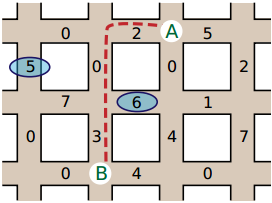
第三個人出現在交會處 A = (0, 2),並且希望逃到交會處 B = (2, 1)。現在她遇到的袋熊數量最少會是 5,如新的虛線所示。
Problem Source
IOI 2013
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 1~8 | 9 |
| 3 | 9~17 | 12 |
| 4 | 18~23 | 15 |
| 5 | 24~27 | 18 |
| 6 | 28~31 | 21 |
| 7 | 32~39 | 24 |
