1766 . Ch3. Section 1. 本營邁進
Tags
Description
在控制室發現了原來控制學校所有師生的原來就是鐘聲...
妁艷馬上將鐘聲給破壞掉了,把控制室中所有人也都給解放了...
「楓音,就這樣!」妁艷回頭一看,發現楓音整個人不停的顫抖,露出了惶恐的表情
「楓音...你...怎麼了?」妁艷十分緊張的扶著
只見楓音一跪,妁艷也立刻察覺到了不對勁
「妁艷...妁艷...那邊...好像有什麼...好...強的壓迫感」楓音不停的顫抖著
妁艷也感覺到就在校園的那個角落...好像有股十分強大的魔力
緊緊的抱著楓音,妁艷也感覺到了十分的不安
但是那強大的魔力一下就又消失了。
妁艷扶著楓音緩緩的走向剛剛那個魔力的來源─圖書館。
用著顫抖的手掌,緩緩的推開了圖書館的大門。
進去之後的感覺跟平常似乎沒什麼不一樣,妁艷慢慢地深入,想要從之中在搜尋一些線索...
此時楓音又開始發抖「妁艷...妁艷...不要...前面那個地方...的魔力讓我好不舒服...」
正當妁艷感到納悶的時候,圖書館樓上突然出現了一個蘿莉...
「嗯...很厲害呢!可是已經為時已晚了!」

瞬間,就在楓音剛剛指的那個地方爆出了一個像是祭壇一般的東西,上面不停得冒著源源不絕的...魔力漿
「這東西...這...哪來這麼多的魔力集合...」
原本圖書館的地板也裂出了一道一道的縫...並且都延伸到了圖書館的底端。
留著魔力漿的裂縫的底端是很多個皿所擺成的魔法陣(意味著所有的魔力漿都流向皿中,當然皿也可能分泌魔力漿至其他皿中)
「這很明顯是個陷阱阿!我怎麼沒發現到這根本是個咒式阿!」妁艷懊悔的想著...
「哈哈哈!你就乖乖的落入這...嘿嘿嘿」,蘿莉說完便消失了。
妁艷仔細一看,知道以楓音現在的狀況他們根本不可能阻止魔力漿的流出...
「看來只能盡量降低這咒式的強度了!」妁艷心想...
他發現裂縫跟裂縫中間都有著轉折點,而且每條裂縫的單位時間能流過的魔力漿也是固定的
他還發現中央的祭壇只是不停的在加大整個強大的魔法陣的強度而已,而每個轉折點則緩緩的留出魔力漿來灌入皿中以準備啟動它
妁艷還知道,當漿盛滿了皿後,整個咒式就會開始啟動。
現在給你每個轉折點跟轉折點之間(或轉折點與皿或是皿與皿之間)的裂縫可以流過的魔力漿流量,
問你所有皿跟轉折點中,到其他所有皿中最多的魔力漿流量可能是多少?妁艷只要能破壞這個轉折點或是皿...就能大大降低咒式的威力了。
Input Format
第一行有一個
接下來N-1每行會有
對於所有測資,
PS.你可以假設他的連接跟一棵樹一樣噢~
Output Format
輸出從一個轉折點或皿到其他所有皿的最大流量
Sample Input 1
5 1 2 11 1 4 13 3 4 5 4 5 10
Sample Output 1
26
Hints
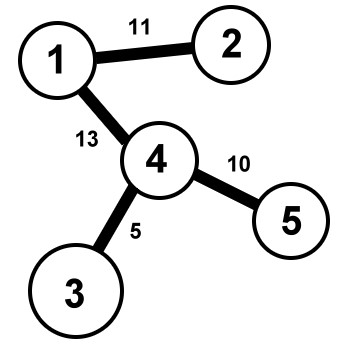
這個情況就能得到
皿的位置是2,3,5
而從1可以留到2的流量有11,到3有5(瓶頸在3<->4之間),到5有8(因為到3已經用去了5,所以瓶頸是在1<->4之間的(13-5)才對而非4<->5間的10)
故1的可流出的容量為11+5+8=24
此例最多的位置是4,可以流出5(4<->3)+10(4<->5)+11(4<->1<->2)=26
其他:
1.請別用奧步解...
2.也有人把皿稱為葉子
Problem Source
原TIOJ1766 / problem setter: jeremy89183
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 6 |
| 2 | 1 | 6 |
| 3 | 2 | 6 |
| 4 | 3 | 6 |
| 5 | 4 | 6 |
| 6 | 5 | 6 |
| 7 | 6 | 6 |
| 8 | 7 | 6 |
| 9 | 8 | 6 |
| 10 | 9 | 6 |
| 11 | 10 | 6 |
| 12 | 11 | 6 |
| 13 | 12 | 6 |
| 14 | 13 | 6 |
| 15 | 14 | 6 |
| 16 | 15 | 10 |
