1748 . [APIO '11] Color

Submit
Status
Discussion / Solution
Ranklist
Back to Problems List

TopCoder

Caido
$\mathbb{W}\mathcal{aimai}\sim$

User's AC Ratio

90.5% (19/21)

Submission's AC Ratio

38.2% (42/110)

Tags

APIO 2011-APIO

Description

Sam和他的妹妹Sara 有一個包含n × m 個方格的表格。
她們想要將其的每個方格都染成紅色或藍色。
出於個人喜好，他們想要表格中每個2 × 2 的方形區域都包含奇數個（1 個或3 個）紅色方格。
例如，下圖是一個合法的表格染色方案。

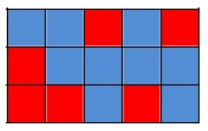
可是昨天晚上，有人已經給表格中的一些方格染上了顏色！現在 Sam 和 Sara非常生氣。
不過，他們想要知道是否可能給剩下的方格染上顏色，使得整個表格仍然滿足她們的要求。
如果可能的話，滿足他們要求的染色方案數有多少呢？

Input Format

輸入的第一行包含三個整數n, m 和k，分別代表表格的行數、列數和已被染色的方格數目。
之後的 k 行描述已被染色的方格。
其中第i 行包含三個整數xi, yi和ci，分別代表第i 個已被染色的方格的行編號、列編號和顏色。
ci為 1 表示方格被染成紅色，ci為 0 表示方格被染成藍色。

對於20%的測試數據，n, m ≤ 5，k ≤ 5；
對於50%的測試數據，n, m ≤ 5000，k ≤ 25；
對於所有的測試數據，2 ≤ n, m ≤ 105，0 ≤ k ≤ 105，1 ≤ xi ≤ n，1 ≤ yi ≤ m。

Output Format

輸出一個整數，表示可能的染色方案數目W 模109得到的值。
（也就是說，如果 W 大於等於 109，則輸出 W 被 109除所得的餘數）。

Sample Input 1

3 4 3
2 2 1
1 2 0
2 3 1

Sample Output 1

8

Hints

Problem Source

原TIOJ1748 / APIO '11

Subtasks

No. Testdata Range Score
1 0 3
2 1 3
3 2 3
4 3 3
5 4 3
6 5 3
7 6 3
8 7 3
9 8 3
10 9 3
11 10 3
12 11 3
13 12 3
14 13 3
15 14 3
16 15 3
17 16 3
18 17 3
19 18 3
20 19 3
21 20 3
22 21 3
23 22 3
24 23 3
25 24 3
26 25 3
27 26 3
28 27 3
29 28 3
30 29 13

Testdata and Limits

No. Time Limit (ms) Memory Limit (VSS, KiB) Output Limit (KiB) Subtasks
0 3500 65536 262144 1
1 3500 65536 262144 2
2 3500 65536 262144 3
3 3500 65536 262144 4
4 3500 65536 262144 5
5 3500 65536 262144 6
6 3500 65536 262144 7
7 3500 65536 262144 8
8 3500 65536 262144 9
9 3500 65536 262144 10
10 3500 65536 262144 11
11 3500 65536 262144 12
12 3500 65536 262144 13
13 3500 65536 262144 14
14 3500 65536 262144 15
15 3500 65536 262144 16
16 3500 65536 262144 17
17 3500 65536 262144 18
18 3500 65536 262144 19
19 3500 65536 262144 20
20 3500 65536 262144 21
21 3500 65536 262144 22
22 3500 65536 262144 23
23 3500 65536 262144 24
24 3500 65536 262144 25
25 3500 65536 262144 26
26 3500 65536 262144 27
27 3500 65536 262144 28
28 3500 65536 262144 29
29 3500 65536 262144 30
Submit
Back to Top