1746 . [APIO '10] Patrol
TopCoder
Description
在一個城市裡,有N個編號從1、2、至N的村莊,而有N-1條路連接著這些村莊。
每條路都確實連接2個村莊,人們都可以利用這些路從任何一個村莊到達其他村莊。每條路的長度為1單位。
為了確保這個城市居民的安全,城市警察巡邏隊必須每天巡查每條路。
警察局在1號村莊,所以巡邏隊必須從1號村莊出發,到最後也必須回到1號村莊。
以下列擁有8個村莊的城市為例,可以看到村莊排列如同圖形,而那個黑色圓形即是1號村莊。
連接著村莊的路就是那些線。要巡查所有道路,巡邏隊每天必須走過14條路。
注意! 每條道路巡邏隊必須走過兩遍才能完成每天的任務。

為了減少每天必須走過的總距離,這個城市計畫在村莊間興建一條新捷徑K。
每條捷徑可以連結任兩個村莊。兩條捷徑可以在同一個村莊會合 (如同下圖的c)。
一條捷徑也可以是一個環狀,也就是說,連結該村莊本身。
由於經費有限,因此,捷徑K必須是1條或2條。
而且,為了確保該城市沒有浪費金錢,巡邏隊在一天中必須走過每條捷徑一次。
以下是可以考慮的可能性。
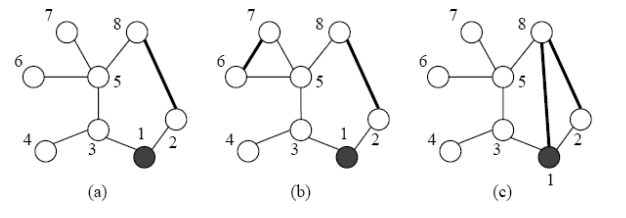
在可能性(a)中,只興建一條捷徑,總距離為11。
在可能性(b)中,興建兩條捷徑,巡邏隊必須走過10單位路線。
在可能性(c)中,興建兩條捷徑,可是因為有次數規定巡邏隊需走過捷徑一次,因此總距離變成15。
請寫一個關於連結村莊間的道路與欲興建的捷徑數量的程式,並且估算捷徑的所在地讓巡邏隊每天需巡查的總距離為最短。
Input Format
輸入的第一列包含兩個整數N和K (1 ≦ K ≦ 2)。下一個N-1列包含道路資訊,
每一列都包含兩個整數A和B (1 ≦ A, B ≦ N),亦即村莊A和村莊B都有一條路可以連接。
•在 10%的測試案例中,N ≦ 1000 且 K = 1。
•在 30%的測試案例中,K = 1。
•在 80%的測試案例中,相鄰村莊的最大值是25。
•在 90%的測試案例中,相鄰村莊的最大值是150。
•在100%的測試案例中,3≦ N ≦100000 且 1 ≦ K ≦2。
Output Format
你的程式輸出結果為一個整數,讓捷徑K被興建後,巡邏隊可以以最短的距離巡查城市。
Sample Input 1
8 1 1 2 3 1 3 4 5 3 7 5 8 5 5 6
Sample Output 1
11
Sample Input 2
8 2 1 2 3 1 3 4 5 3 7 5 8 5 5 6
Sample Output 2
10
Sample Input 3
5 2 1 2 2 3 3 4 4 5
Sample Output 3
6
Hints
Problem Source
原TIOJ1746 / APIO '10
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 3 |
| 2 | 1 | 3 |
| 3 | 2 | 3 |
| 4 | 3 | 3 |
| 5 | 4 | 3 |
| 6 | 5 | 3 |
| 7 | 6 | 3 |
| 8 | 7 | 3 |
| 9 | 8 | 3 |
| 10 | 9 | 3 |
| 11 | 10 | 3 |
| 12 | 11 | 3 |
| 13 | 12 | 3 |
| 14 | 13 | 3 |
| 15 | 14 | 3 |
| 16 | 15 | 3 |
| 17 | 16 | 3 |
| 18 | 17 | 3 |
| 19 | 18 | 3 |
| 20 | 19 | 3 |
| 21 | 20 | 3 |
| 22 | 21 | 3 |
| 23 | 22 | 3 |
| 24 | 23 | 3 |
| 25 | 24 | 3 |
| 26 | 25 | 3 |
| 27 | 26 | 3 |
| 28 | 27 | 3 |
| 29 | 28 | 3 |
| 30 | 29 | 13 |
