1738 . [APIO '07] Zoo
Description
新落成的環狀動物園是亞太地區之新驕傲。它座落於太平洋的小島,其造型是由不同的獸檻環繞而成的大圓環,
每一獸檻內珍奇的動物皆不相同,如下圖所示。
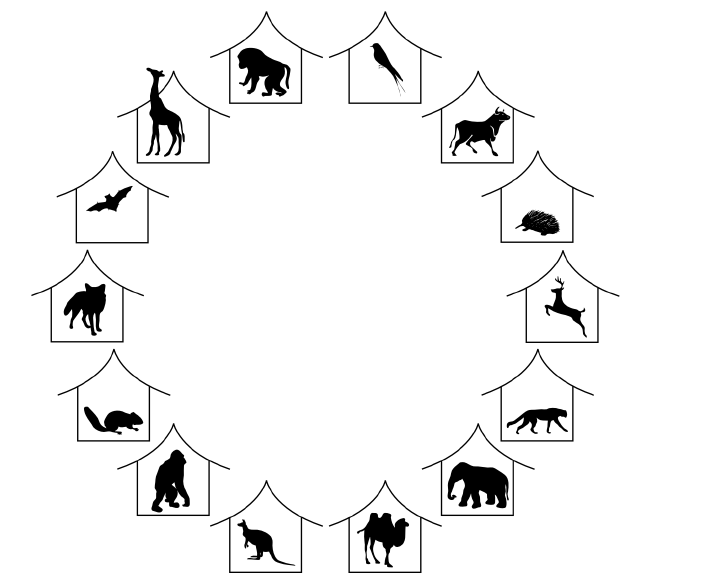
你是動物園的公關負責人,也就是說你的工作就是要盡量的讓訪客高興。滿載著學童的巴士剛抵達,而你熱切期
盼能讓他們高興。不過,這不是件容易的事 。 有些動物受到某些孩童喜愛,而某些動物讓有些孩童害怕。例如,
小Alex 喜愛猴子和無尾熊因為它們很可愛,但因為獅子有利牙而怕它們。相反的,Polly 喜愛獅子因為它們有
美麗的鬃毛,但因為無尾熊的味道而怕它們。
你可以選擇將一些獸檻內的動物移走,以避免孩童害怕。不過又擔心如果移走了太多的動物,那孩童就沒有
什麼可看的了。你的任務是決定移走哪些動物以使高興的孩童越多越好。
所有的孩童都站在獸檻環的外面,每一個都可以看到相連的五個獸檻。你手上有一張清單,列出了每一個孩
童喜歡的動物們及害怕的動物們。讓孩童高興的條件為:
(i)至少有一隻在他們的視線內使他們害怕的動物被移走了。或者
(ii)至少有一隻在他們的視線內他們所喜愛的動物沒有被移走。
例如,考慮如下所示的孩童與動物的位置以及孩童之好惡清單:
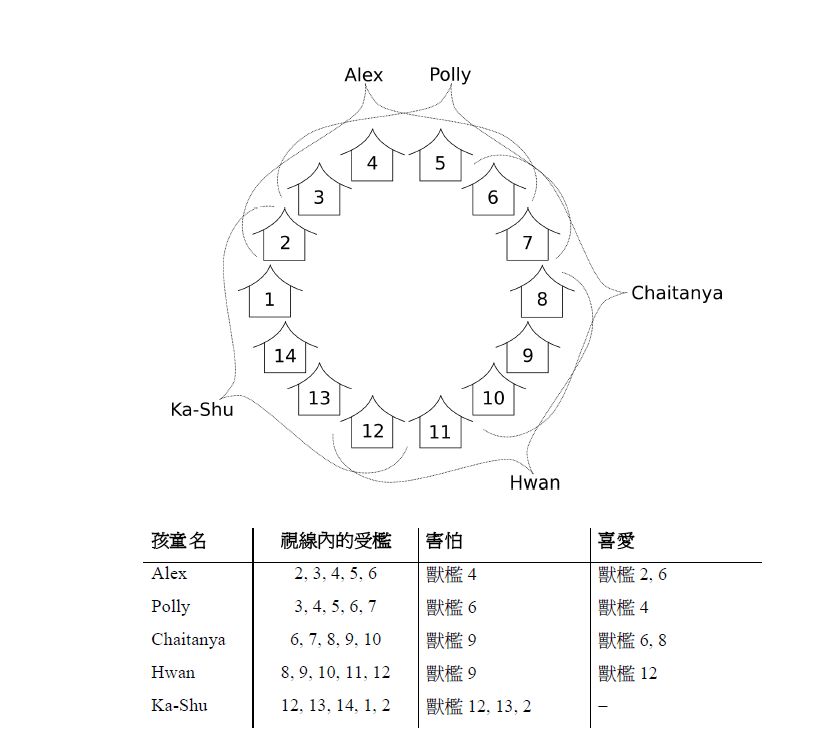
假設你將4 號和12 號獸檻內的動物移走。這將使Alex 和Ka-Shu 感到高興,因為至少有一隻他們害怕的
動物被移走了。這此安排仍能使Chaitanya 高興,因為他所喜愛的6號及8 號獸檻裡面的動物還在。不過Polly
和Hwan 將會不高興,因為他們沒有辦法看到任何喜愛的動物,而他們所害怕的動物卻仍然都還看得到。考慮另外
一種情形,不移走4 號及12 號獸檻裡的動物,而是移走4 號及6 號獸檻裡的動物。Alex 和Polly 會因此而高
興因為在4 號及6 號獸檻內令他們害怕的動物被移走了。Chaitanya 也仍會高興,因為雖然6 號獸檻內他喜愛
的動物被移走了,他仍能看到8 號獸檻內他喜愛的動物。同樣的,Hwan 也會高興,因為現在可以看到12 號獸檻內
他所喜愛的動物了。唯一不高興的人將會是Ka-Shu。
最後,考慮不移走4 號和6 號獸檻裡的動物,而只移走13 號獸檻內的動物。現在Ka-Shu 高興了,因為他所
害怕的動物被移走了,而且Alex,Polly,Chaitanya 和Hwan 也都高興,因為他們都至少能看到一隻喜愛的動
物。因此這樣的安排會使五個孩童高興,這當然也是所有可能情形中最佳的情形。
Input Format
第一行的形式為
獸檻以順時鐘方向編號為
接下來還有
每一行的形式如下:
其中:
- 獸檻號碼
- 獸檻號碼
- 整數
孩童的資料將以依照其第一個可見獸檻
Output Format
為一整數,是所有安排中感到高興的孩童數之最大值
Sample Input 1
14 5 2 1 2 4 2 6 3 1 1 6 4 6 1 2 9 6 8 8 1 1 9 12 12 3 0 12 13 2
Sample Output 1
5
Hints
Problem Source
原TIOJ1738 / APIO '07
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 5 |
| 2 | 1 | 5 |
| 3 | 2 | 5 |
| 4 | 3 | 5 |
| 5 | 4 | 5 |
| 6 | 5 | 5 |
| 7 | 6 | 5 |
| 8 | 7 | 5 |
| 9 | 8 | 5 |
| 10 | 9 | 5 |
| 11 | 10 | 5 |
| 12 | 11 | 5 |
| 13 | 12 | 5 |
| 14 | 13 | 5 |
| 15 | 14 | 5 |
| 16 | 15 | 5 |
| 17 | 16 | 5 |
| 18 | 17 | 5 |
| 19 | 18 | 5 |
| 20 | 19 | 5 |
