你經營一家資訊科技公司它專為大型辦公室從事電腦資料備份服務。但是資料備份並不是一件容易的事，
因此你設計了一個系統讓不同辦公室間能自動備份彼此間的資料，這樣你才有空閒回家打電動。

　　這些辦公室都坐落在同一條街道上。你決定把這些辦公室兩兩分成一對，並且在每一對辦公室所在的兩棟
大樓之間鋪設網路電纜連接它們，使得它們可以備份彼此的資料。

　　然而，網路電纜是很昂貴的。當地的電信公司將只會提供給你k 條網路電纜，這意謂你只能安排 $k$ 對辦公
室的備份（總共有 $2k$ 個辦公室）。每一個辦公室最多只能與另一個辦公室配對（也就是說，這些 $2k$ 個辦公室
都必須是不同的）

　　再者，電信公司是論公里收費。這意謂這 $k$ 對辦公室配對選擇必須使用越短的電纜越好。換句話說，所有
配對辦公室的電纜長度加總後要越少越好。

　　舉例來說，假設你有5 個客戶的辦公室是坐落在同一條街，如下圖所示。這些辦公室分別坐落在離街道起
點的1 公里、3 公里、4 公里、6 公里以及12 公里處。電信公司將只會供給你 $k=2$ 條電纜。

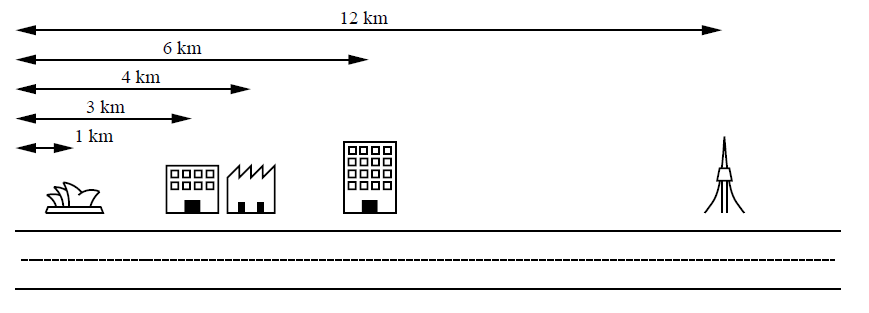
　　在這個問題中最好的配對方式是把第一個與第二個辦公室間連接在一起、第三個與第四個辦公室連接在一起。
這樣就符合需求使用 $k=2$ 條電纜，其中第一條電纜的長度為 3 公里 - 1 公里 = 2 公里、第二條電纜的長度為 6 公里 - 4 公里 = 2 公里。
這個配對方式總共需要 4 公里的網路電纜，這也是電纜總長度需求最少的配對方式。