1736 . [APIO '07] Mobiles
Description
你需要幫你的弟弟艾克買禮物。艾克對禮物有很特殊的品味,而且他只喜歡能調整成他喜好樣子的禮物。
你發現了一間賣吊飾的禮品店。這裡所謂的吊飾是一種能吊在天花板上的多層裝飾品。一個吊飾由許多
橫桿藉由垂直連接線連接而成。每一根橫桿的兩頭都連有線,可掛上另一根橫桿,或是一個玩具。以下以圖
示表示一個吊飾。

如果想讓艾克接受一個吊飾做為禮物,此吊飾必須能經由調整,從而滿足以下條件:
(i) 任意兩個玩具必須在同樣的高度,或是高度僅差一。在這裡所謂的高度是指
禮物到達天花板所需經過的橫桿數。
(ii) 對任意兩個高度差一的禮物而言,左邊的禮物必須比較低。
吊飾可經由所謂交換進行調整。互換的具體定義是選定一個橫桿,取下兩端所掛的東西,左右交換之後
再掛回原選定的橫桿。此一動作並不會改變我們從選定的橫桿兩端所取下的東西其內部物件(橫桿或玩具)
的順序。
因為你正在接受資訊奧林匹亞集訓,所以你決定寫一個程式來決定一個給定的吊飾是否能經由互換
而調整成艾可會喜歡的形式。
考慮上面的吊飾圖例。艾可不會喜歡這個吊飾。雖然它滿足第一個條件,但並不滿足
第二個條件–最左邊的玩具比他右邊的玩具來的高。
雖然如此,這個吊飾還是可以調整成艾可喜歡的形式。我們需要進行以下步驟:
1. 首先,交換橫桿
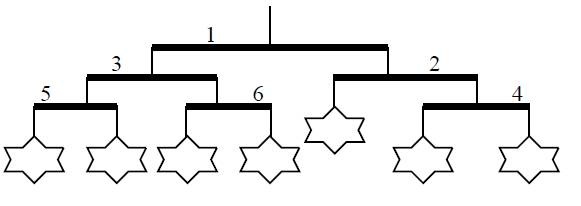
2. 接著我們交換橫桿
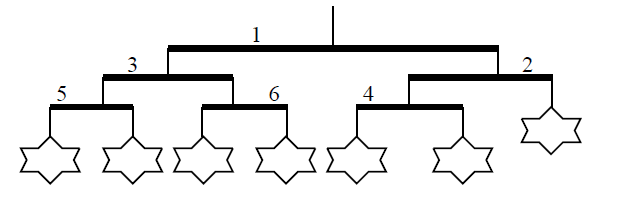
經由這些調整,此吊飾可以滿足艾可喜歡的條件。意即所有的玩具高度最多差一,而
且比較低的玩具會在比較高的玩具左邊。
你的工作是當給定一個吊飾時,找出最小數目的互換動作將吊飾調整成艾可喜歡的樣
子(如果可能的話)。我們在此假定玩具在調整過程中不會互相卡住。
Input Format
輸入的第一行為一整數
接下來的
情形。這裡每一行有兩個整數
左右兩端所掛的東西。如果此整數為
整數的橫桿。
如果編號為
的橫桿。
Output Format
輸出為一行,且此行僅有一整數,代表將此吊飾調整成艾可喜歡樣子所需的最少互換
數目。如果此吊飾不可能調整成艾可喜歡的樣子則輸出
Sample Input 1
2 3
-1 4
5 6
-1 -1
-1 -1
-1 -1
Sample Output 1
Hints
Problem Source
原TIOJ1736 / APIO '07
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 2 |
| 2 | 1 | 2 |
| 3 | 2 | 2 |
| 4 | 3 | 2 |
| 5 | 4 | 2 |
| 6 | 5 | 2 |
| 7 | 6 | 2 |
| 8 | 7 | 2 |
| 9 | 8 | 2 |
| 10 | 9 | 2 |
| 11 | 10 | 2 |
| 12 | 11 | 2 |
| 13 | 12 | 2 |
| 14 | 13 | 2 |
| 15 | 14 | 2 |
| 16 | 15 | 2 |
| 17 | 16 | 2 |
| 18 | 17 | 2 |
| 19 | 18 | 2 |
| 20 | 19 | 2 |
| 21 | 20 | 2 |
| 22 | 21 | 2 |
| 23 | 22 | 2 |
| 24 | 23 | 2 |
| 25 | 24 | 2 |
| 26 | 25 | 2 |
| 27 | 26 | 2 |
| 28 | 27 | 2 |
| 29 | 28 | 2 |
| 30 | 29 | 2 |
| 31 | 30 | 2 |
| 32 | 31 | 2 |
| 33 | 32 | 2 |
| 34 | 33 | 2 |
| 35 | 34 | 2 |
| 36 | 35 | 2 |
| 37 | 36 | 2 |
| 38 | 37 | 2 |
| 39 | 38 | 2 |
| 40 | 39 | 2 |
| 41 | 40 | 2 |
| 42 | 41 | 18 |
