1724 . SpaceChem
TopCoder
Tags
Description
SpaceChem王國是個以出口各種化學分子為業的工業型國家。
他們常常在一個城市設置一個大工廠,進行組合和拆解分子,甚至是核分裂和融合!
然後再透過各種管道運到下一個工廠加工,最後再透過空運或海運送出口。
過了近百年的輝煌時期,最近SpaceChem王國由胖胖蚯金國王登上了王位。
新王上任總要推行一些親民政策奠下統治的基礎,於是就調降稅賦啦。
胖胖蚯金國王一面吃著楓糖冰一面思考:"要調降多少稅勒? 50%如何? 好像太少了,那就99%吧"
就這樣,稅賦不小心降過了頭,王國的收入突然變得相當少,財政陷入了危機。
既然沒辦法開源,那就節流吧。
於是胖胖蚯金國王打算從支出下手,首先被看上的是維護各條輸送管的維修支出。
SpaceChem王國有
有些管路是用鈦合金管舖設的,有些道路則是用黏土鋪設的!?
鈦合金管路有
胖胖蚯金國王打算刪減管路維修費,他打算只維修一些維護費比較低的管路,但是還是要能使任兩個城市可以透過道路互相往來。
不過計算要維護哪些道路實在是太麻煩了,這是個邪惡的最小生成樹(MST)問題,於是胖胖蚯金國王就把問題扔給了烏龜大臣。
由於烏龜大臣知道鈦合金管比黏土管好很多,所以當維護鈦合金管和維護黏土管的花費相同的時候,他會優先選擇維護鈦合金管。
不幸的是,胖胖蚯金國王對於鈦合金管和黏土管完全沒有概念,他只下令要讓總維修費最少。
但烏龜大臣知道,如果某些城市只能透過黏土管運輸東西,那可能會造成很可怕的後果。輕則氣爆,重則核爆。
你是個管路維修商,負責整個王國的管路維護。
但是為了人民的利益,烏龜大臣私下命令你整修的都是鈦合金管,但胖胖蚯金國王要求花最少錢。
你知道這兩個要求是互相牴觸的。
你只好偽造一些道路的維修費用,使得這兩個要求能夠同時成立。
第i條路的需要花
為了避免烏龜國王懷疑你貪汙或是你虧損太嚴重,
你希望讓
Input Format
每個測資檔只有單筆測資。
第一行有兩個整數
接下來的
前
Output Format
輸出僅有一個數字,最小的
Sample Input 1
5 7 1 2 6 2 3 2 2 4 5 4 5 7 3 4 3 3 5 2 1 5 4
Sample Output 1
9
Sample Input 2
4 5 4 1 7 2 1 5 3 4 4 4 2 5 1 3 1
Sample Output 2
6
Hints
對第一筆Sample,
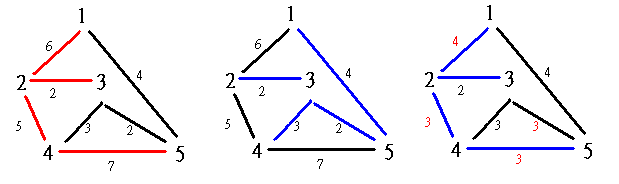
第一張圖是原圖,紅色表示鈦合金管,黑色表示泥土管。
第二張圖的藍色邊是基於最小花費的情況下,打算維護的的管路。
第三張圖是經過偽造部分管路的費用後,基於最小花費的情況下,打算維護的道路。
成功的讓所有被維護的管路都是鈦合金管。
且這個修改方案會使
Added
Problem Source
原TIOJ1724 / Problem Setter : yuscvscv
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 4 |
| 2 | 1 | 4 |
| 3 | 2 | 4 |
| 4 | 3 | 4 |
| 5 | 4 | 4 |
| 6 | 5 | 4 |
| 7 | 6 | 4 |
| 8 | 7 | 4 |
| 9 | 8 | 4 |
| 10 | 9 | 4 |
| 11 | 10 | 4 |
| 12 | 11 | 4 |
| 13 | 12 | 4 |
| 14 | 13 | 4 |
| 15 | 14 | 4 |
| 16 | 15 | 4 |
| 17 | 16 | 4 |
| 18 | 17 | 4 |
| 19 | 18 | 4 |
| 20 | 19 | 4 |
| 21 | 20 | 4 |
| 22 | 21 | 4 |
| 23 | 22 | 4 |
| 24 | 23 | 4 |
| 25 | 24 | 4 |