1618 . 城市景觀問題
TopCoder
Tags
Description
小蚯蚓是一個旅行家，他到了一個稱作Linear City的地方。
這個城市共有n棟建築。所有建築物都是高樓大廈，每棟都有高度Hi跟美觀度Bi。
依序排成一條直線，從左到右編號為1~n。
小蚯蚓想要選一個景觀很好的地方慢慢欣賞風景(也就是那些建築物)。
但是，小蚯蚓有閃光(一種眼疾，會看東西看得很不清楚)，頂多只能看到距離k以內的建築物。
而且建築物也可能會被其他建築物擋住。
也就是一棟建築物會被看到的充要條件就是：
1.該建築物跟小蚯蚓的距離要在k以內
2.該建築物到小蚯蚓之間任何建築物都只能比該建築物低(相等也是看不到的喔!)
他發明了一個函式可以估計該點的風景美觀度，也就是View(p) 其中1<=p<=n。
所謂View(p)就是，站在建築物p的右邊往左看。所有看得到的建築物的美觀度加起來。
例如下圖就是在n=9, k=4下計算得View(6)=4
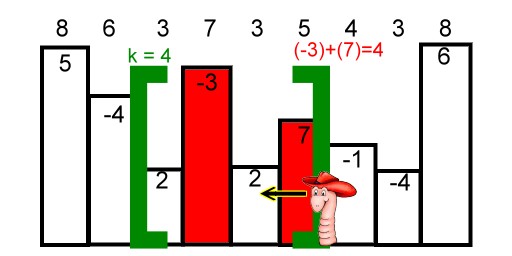
現在小蚯蚓想問你他站在哪裡才能得到最大的View()值？
Input Format
第一行有兩個數字n, k表示這個城市的建築數目以及小蚯蚓的視力範圍。
第二行有n個數字，第i個數字Hi表示建築物i的高度，
第三行有n個數字，第i個數字Bi表示建築物i的美觀度。
1 <= n <= 500,000;
1 <= k <= n;
1 <= Hi<= 1,000,000,000
-1000 <= Bi <= 1000
Output Format
輸出在同一行內包含兩個數字p q，以空白分開。
表示站在p的位置時View(p)=q 有風景美觀度的最大值。
若有很多個p的View()相同，輸出最小的那個。
Sample Input 1
9 4
8 6 3 7 3 5 4 3 8
5 -4 2 -3 2 7 -1 -4 6
8 6 3 7 3 5 4 3 8
5 -4 2 -3 2 7 -1 -4 6
Sample Output 1
9 6
Hints
很久以前一直以為散光寫作閃光...
對了，範測就是那張圖。
這題用cin絕對會超時
Problem Source
原TIOJ1618 / Problem Setter：ATP
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 16 |
| 2 | 1 | 16 |
| 3 | 2 | 16 |
| 4 | 3 | 16 |
| 5 | 4 | 16 |
| 6 | 5 | 20 |