1608 . Problem B 登山法 (CLIMBU)
TopCoder
Tags
Description
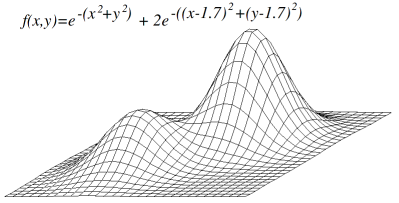
登山法(Hill Climbing)是狀態空間搜索的一種方法。
假設在我們要最佳化的問題的狀態可以用座標 (x, y) 來表示,且對於任一個狀態 (x, y) (1 ≤ x ≤ n,1 ≤ y ≤ m,x, y∈N),
其價值皆可以用f(x, y) 來計算,那登山法的目的就是找到座標 (x*, y*) 使得 f(x*, y*) 最大。
登山法的起始點 (x', y') (1 ≤ x' ≤ n,1 ≤ y' ≤ m,x', y'∈N)是隨機選定的。
接著在每一步的迭代之中,程式會選擇相鄰的四個座標 (x'-1, y')、(x'+1, y')、(x', y'-1)、(x', y'+1)當中價值最高的一個「走過去」。
整個過程就好像爬山一樣。當然,迭代的終止條件是程式所在位置的價值不小於任一相鄰座標的價值。
顯然登山法最大的缺點就是會陷入「區域最優解」之中,也就是走不到在整個範圍內最高的一個點(全域最優解)。
現在,給你所有狀態 (x, y) 的價值 f(x, y),請問有多少個起點走不到全域最優解呢 ?
當相鄰的座標價值相同時,請依照 (x'-1, y') → (x'+1, y') → (x', y'-1) → (x', y'+1) 的順序優先選擇。
Input Format
輸入的第一行是兩個正整數,代表n, m。(2≦n,m≦1,000)
接下來的n行,每行有m個整數,第i+1行的第j個整數代表 f(i, j)。
-230≦f(i, j)≦230。
對於所有未指定的座標 (x, y),f(x, y) = -∞。
Output Format
輸出一行,代表在這 n*m 個起點當中,有多少個走不到全域的最優解。
Sample Input 1
3 6 1 3 5 7 6 8 -1 5 30 4 3 9 8 11 3 2 4 6
Sample Output 1
10
Hints
Problem Source
原TIOJ1608 / Problem Setter: suhorng
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 10 |
| 2 | 1 | 10 |
| 3 | 2 | 10 |
| 4 | 3 | 10 |
| 5 | 4 | 10 |
| 6 | 5 | 10 |
| 7 | 6 | 10 |
| 8 | 7 | 10 |
| 9 | 8 | 10 |
| 10 | 9 | 10 |
