1569 . 8 Puzzle - the Hyper version
Description
玩過 8 Puzzle 遊戲嗎? 這種 3x3 缺一格的拼圖遊戲可說是歷久不衰,也有各式各樣的版本,
從最一開始的 1, 2, 3, ..., 8 的純數字到打散的圖片面板,無論是哪種都讓人一玩就上手且不自覺的著迷其中。
這種經典遊戲的規則是,一開始給你一個打散(Shuffle)過後的盤面(State),要你利用那唯一的空格所能產生的各種影響,
即將其上、下、左、右四個方位的拼圖移至該空格,想辦法讓整個盤面復原成初始盤面(Solved State),
然而,復原回初始盤面的方法有很多種,所以人們通常希望能用盡量少的步驟(Step)就能復原完成。
然而,隨著時代的進步,越來越多人覺得單純的 8 Puzzle 太容易解決了,沒有挑戰性!
所以不知道是誰就發明了一種進階版的 8 Puzzle,這種新型的 8 Puzzle 遊戲外觀跟舊版的相去不遠,
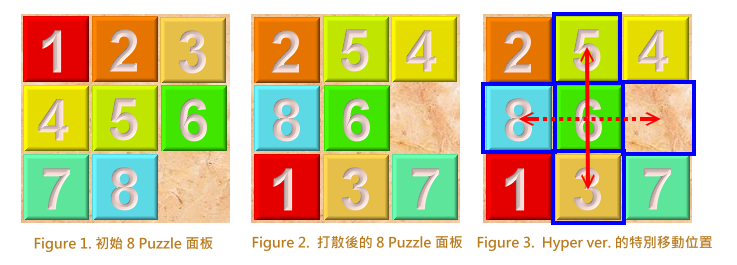
唯一的差別是,你可以將正上方、正左方、正右方、正下方這四格的數字移動到正下方、正右方、正左方、正上方!(詳見下面例圖的藍色框線)
這下有趣了,多了這幾個步驟後,可以想見的是這遊戲反而變得更加容易了!因為你有更多的移動選擇。
那究竟為什麼這項改變會使人們又恢復了對於這個傳統遊戲的熱情呢?
原因就在於,雖然整體難度變簡單了,但是若是要達到「最小步驟數復原」就變得更加困難了,原因一樣是由於選擇性變多了。
因此,現在就請你針對這種新型的 8 Puzzle 遊戲寫一個程式,
對於每個給定的盤面,計算出最少需要多少步驟才能夠復原完成。
注意: 可能會有無法復原完成的盤面!!
Input Format
每筆測試資料都包含了一個 8 Puzzle 盤面,
對於每個盤面,都是以 3x3 的方式表示(如範例輸入),空格的部分以 0 代替。
你可以相信輸入中不會有不合法的盤面出現。
Output Format
請輸出一個正整數,代表對於給定的盤面若以新的規則進行遊戲,最少必須要花幾個步驟才能將其復原成初始盤面。
若無法復原成原始盤面,請輸出 "Impossible"(不含雙引號)。
Sample Input 1
4 5 6
0 7 8
Sample Output 1
Hints
Scoring:
對於 10% 的測試資料,我們保證答案步驟數 S≦5。對於 30% 的測試資料,我們保證答案步驟數 S≦15。
Problem Source
原TIOJ1569 / 第二屆快樂暑假營 -- 最終練習比賽
Problem Setter: Skyly
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 10 |
| 2 | 1 | 10 |
| 3 | 2 | 10 |
| 4 | 3 | 10 |
| 5 | 4 | 10 |
| 6 | 5 | 10 |
| 7 | 6 | 10 |
| 8 | 7 | 10 |
| 9 | 8 | 10 |
| 10 | 9 | 10 |
