1546 . 填方格遊戲
TopCoder
Tags
Description
有N個人聚在一起(編號為0到N-1),玩一個很神奇的填方格遊戲,規則如下:
(1) 準備由M*M個小正方形格子組成的一個大正方形。
(2) 在這個大正方形的最左邊一欄和最上面一列的每一格都任意填上非負整數,並決定兩個數P, Q(2 ≤ P ≤ Q ≤ M)。
(3) 從第0號開始往後輪(N-1號之後輪回0號),輪到的人必須選擇做(a), (b), (c)三個操作中的其中一個:
(a) 找到左上方、上方、左方格子皆已經有數字的一個空格,將其填上左上、上方、左方格子中數字的XOR值。(如果你不知道什麼是XOR,請往下找藍色字。)
(b) 找到一個填滿數字的1*C橫列並記錄下來。這個橫列必須滿足P ≤ C ≤ Q,並且其中每一個格子的數字都大於等於橫列中它左邊所有格子裡的數字。
(c) 找到一個填滿數字的R*1縱列並記錄下來。這個縱列必須滿足P ≤ R ≤ Q,並且其中每一個格子的數字都大於等於縱列中它上面所有格子裡的數字。
對於(b)和(c),已經紀錄下來的橫列或縱列就不能再記錄了。當然,記錄的橫列或縱列和之前的紀錄只是部分重疊的話是沒有問題的。
(例如有一列的數字是1, 2, 3,P=2、Q=3,則有人記錄了1, 2, 3這個橫列,之後的人不可以再記錄一次1, 2, 3這個橫列,但依然可以記錄1, 2這個橫列。)
(4) 如果(a), (b), (c)三件事都無法做時,輪到的人就輸了。
假設這N個人都很聰明,遊戲過程中都會選擇使自己勝率最大的操作,如果有超過一個勝率最大的操作,則他們會以相等的機率隨機選擇一個;也絕對不會明明還有事情可以做卻找不到。
現在告訴你N、M、P、Q和(2)中格子中填上的所有數字,請你判斷誰輸的機率最大。
(如果覺得難以理解的話,Hints有一個遊戲過程的例子。)
什麼?你說你不知道XOR是什麼?兩個整數的XOR值會是另一個整數。在C/C++裡面,XOR的運算子是^,如果要求a, b兩個數的XOR值,a ^ b就是答案。
如果你要求三個整數的XOR值(像(a)操作),你可以求其中兩個整數的XOR值,然後求得到的答案和剩下整數的XOR值。XOR符合交換律和結合律,所以你不必擔心順序不同會對答案造成影響,也就是你如果要求a, b, c的XOR值,則a ^ b ^ c就是答案了。
你是真的想知道XOR是什麼嗎?如果是請繼續看下去,否則請直接跳到後面看輸入格式。
我們知道任何數都可以表示成二進位,當然在電腦裡,所有的數字都是用二進位表示的。例如:138的二進位表示法是10001010、67的二進位表示法是1000011。
而XOR就是對兩個整數做運算:先把兩個整數換成二進位,按位對齊、補零,然後看看兩個數字的同一位是否相同:兩個相同的為0,不同的為1。
很難懂?舉個例子。假如我們要計算138和67的XOR值,我們先把兩個數字轉換成二進位,然後按位對齊、補零:
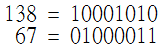
然後一位一位看。兩個數字第一位一個是0、一個是1,兩個不同,因此該位的結果是1:

兩個數字的第二位都是1,相同,該位結果為0:

以此類推,最後得到結果:

轉換回十進位,我們得到138和67的XOR值是201。
另外,Windows提供的小算盤當中,按Alt-3切換到「程式設計師」模式,也有計算XOR的功能喔。
Input Format
第一行有四個正整數N, M, P, Q。如果你不知道這四個數字代表什麼,請回去看題目敘述。
第二行有M個整數,代表從左上角的格子開始,從左到右依序的數字。
第三行有M-1個整數,代表從左上角往下一格的格子開始,從上到下依序的數字。
保證無論遊戲如何進行,每個格子裡面的數字必定會在int範圍內。
| 子任務(測資) | 額外限制 | 分數 |
| 1 (0~3) | 9 | |
| 2 (4~7) | 11 | |
| 3 (8~11) | 19 | |
| 4 (12~15) | 52 | |
| 5 (16~19) | 無 | 9 |
Output Format
輸出一個數字T,代表編號T的人輸的機率最大。如果有兩個人以上輸的機率相同,輸出編號最小的那個人。
Sample Input 1
4 3 2 3 9 1 9 8 3
Sample Output 1
0
Hints
以範例輸入為例,其中一種可能的遊戲發展:
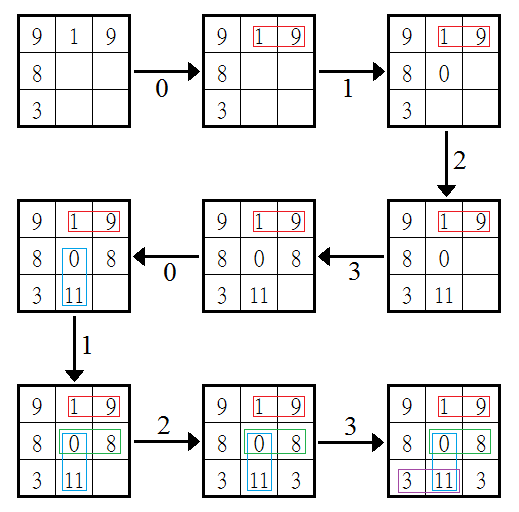
因為0號沒有事情可以做了(所有的格子都被填滿了,而且所有符合條件的橫、縱列都已經被紀錄了),所以在這局當中他輸了。
嗯,你不覺得我有事情沒告訴你嗎?其實這題沒有你想像中的那麼難喔。
Problem Source
Problem set / Description by Yihda Yol
建國中學105學年度校隊選拔:初試pD
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0~3 | 9 |
| 2 | 4~7 | 11 |
| 3 | 8~11 | 19 |
| 4 | 12~15 | 52 |
| 5 | 16~19 | 9 |
