1478 . 樹狀結構展示(Tree)
TopCoder
Tags
Description
樹狀結構為一種程式設計者常用的資料結構,但較不容易在畫面上展示。
常見的樹狀結構展示方式為「樹根在左、樹枝朝右」的橫向目錄型式,但其實若能以「樹根在上、樹枝朝下」的直向表示法,更能展現樹狀結構的精神。而要在電腦的二維螢幕上畫出美觀的樹狀結構,必須計算其中各個節點的座標位置。
以下圖的樹狀結構為例,在一般文字模式的螢幕上(一個位置一個字元),其畫出來的樣子如下所示。其中名稱為N-1 的節點,其起始座標為(5,3),名稱為N-2 的節點,其起始<>座標為(22,3),名稱為N-1-1 的節點,其起始座標為(1,6),其餘依此類推。
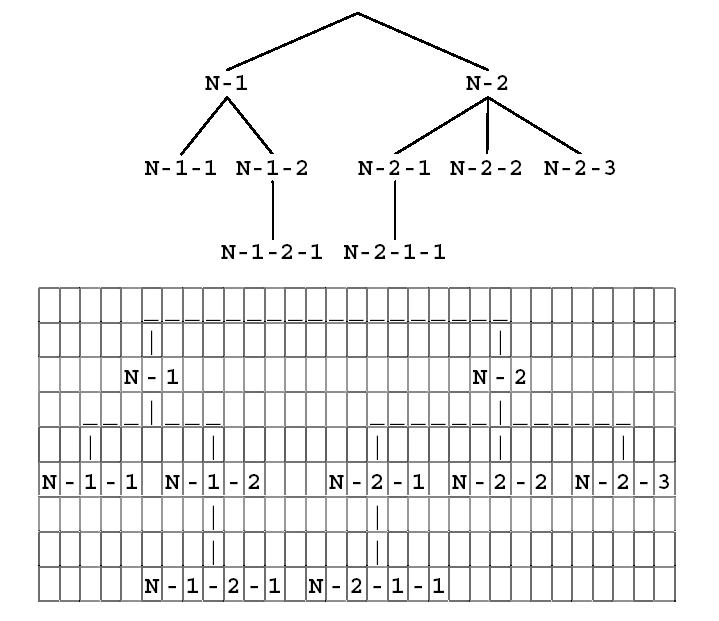
根據上例的表示方法,請寫一程式讀入如下格式的樹狀結構後,轉換為直向的樹狀結
構,輸出每個節點的二維座標位置。
在將輸入轉換成直向的樹狀圖時,為求美觀,轉換時必須符合下列規則:
節點以其名稱輸出。所有的距離、位置、寬度,都以「字元數」計算。
同一階層的節點有相同垂直位置。
同一階層的節點間必須求出最小間隔,但至少距離一個空白字元。
若某一節點有多個子節點,則其水平位置必需在所有子節點的總寬度的正中央。
其計算公式為: S = (1/2)(LS+LE-L)。
其中:
S:本身節點的起始水平位置;當S 無法整除時,取其四捨五入值。
LS:第一個子節點的起始水平位置。
LE:最後一個子節點的最後水平位置。
L:本身子節點的長度。
Input Format
輸入為多行字串,每一行代表一個由根節點到本身節點的路徑,節點名稱由英文、數字與可列印符號表示,而上、下節點之間以冒號隔開。
所有的輸入依照深度優先演算法(Depth-First)列出,不會有如下情形:
N-1
N-1:N-1-1
N-2
N-1:N-1-2
- 輸入格式一定正確,不需考慮輸入格式錯誤情形。
Output Format
輸出時,先輸出每個節點的路徑,其順序輸入相同。
每個路徑後面,空一格後加上括號,括號內第一個值為該節點的起始水平座標位置,第二個值為其垂直座標位置。
水平與垂直座標位置均以字元數計算,由1 開始。如上例中的節點N-1,其起始水平座標位置為5,則輸出5,垂直座標為3,則輸出3。
Sample Input 1
N-1 N-1:N-1-1 N-1:N-1-2 N-1:N-1-2:N-1-2-1 N-2 N-2:N-2-1 N-2:N-2-1:N-2-1-1 N-2:N-2-2 N-2:N-2-3
Sample Output 1
N-1 (5,3) N-1:N-1-1 (1,6) N-1:N-1-2 (7,6) N-1:N-1-2:N-1-2-1 (6,9) N-2 (22,3) N-2:N-2-1 (15,6) N-2:N-2-1:N-2-1-1 (14,9) N-2:N-2-2 (21,6) N-2:N-2-3 (27,6)
Sample Input 2
A A:AB A:AC a a:ab a:ac
Sample Output 2
A (3,3) A:AB (1,6) A:AC (4,6) a (9,3) a:ab (7,6) a:ac (10,6)
Hints
Problem Source
原TIOJ1478 / 96北市賽
建中校內培訓第五次模擬考試。
Problem Setter:hallogameboy、peter50216
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 14 |
| 2 | 1 | 14 |
| 3 | 2 | 14 |
| 4 | 3 | 14 |
| 5 | 4 | 14 |
| 6 | 5 | 14 |
| 7 | 6 | 16 |