1419 . 飛天李晴(?) (Sunny)
TopCoder
Description
飛天桑妮(?)是一隻運動神經很好的鼯鼠,她很喜歡在樹木間移動,尤其最愛從高處一躍而下,享受滑翔的快感。她所居住的森林裡有
從家裡前往奶奶家的旅程可定義為由
由於桑妮想要快點到奶奶家,所以旅程後段的樹木不能比前段的樹木離桑妮家還近,也就是
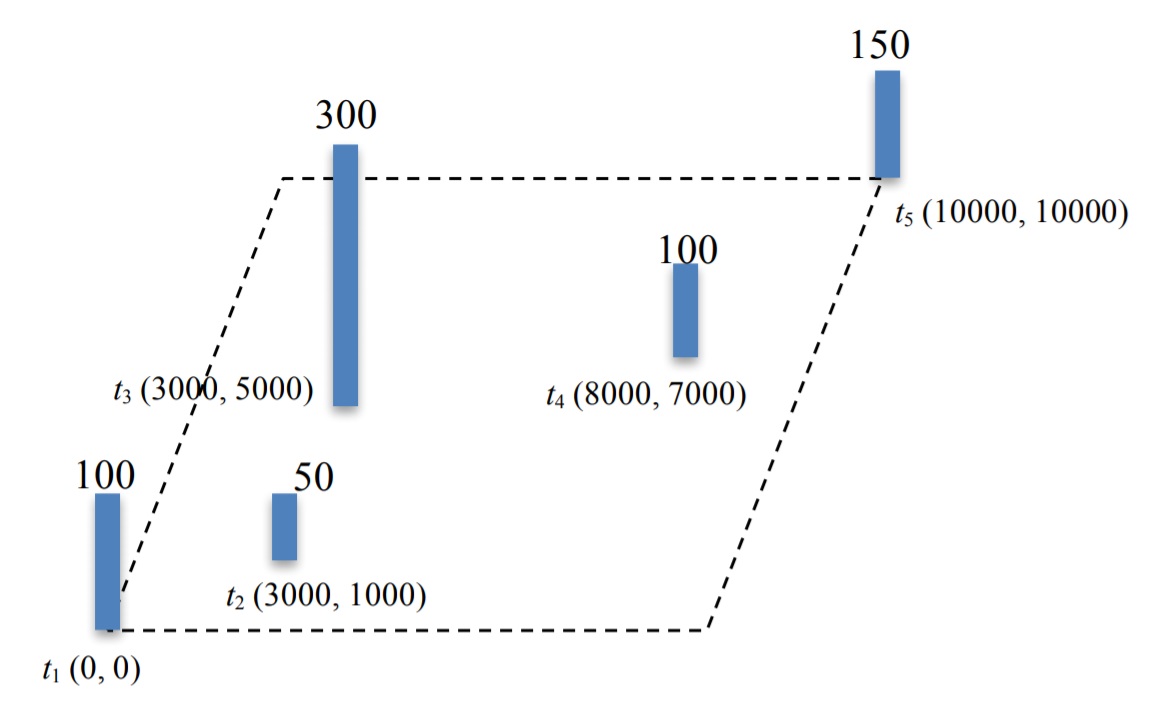
以上圖為例,森林中有五棵樹,其位置和高度如圖所示。如果桑妮的旅程是
Input Format
第一列有一個正整數
Output Format
請輸出所有合理旅程中,最大的樂趣值。
Sample Input 1
7 0 0 42 5726 1480 29359 6965 4465 5706 8148 3284 16828 6335 6503 19170 9962 492 2996 10000 10000 18468
Sample Output 1
26363
Hints
Problem Source
臺北市105學年度高級中學資訊學科能力競賽程式設計試題第一題
Set by Yihda Yol
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0~2 | 30 |
| 2 | 0~6 | 30 |
| 3 | 0~11 | 40 |
