1405 . [Interactive] 神秘的鏡子盒
TopCoder
Description
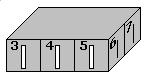
數學家 Andris 有一個小小盒子,盒子的底部分成了 n*m 的格子,每一個格子都可以放一面左下到右上方向的45度雙面鏡。
在盒子的邊界,每行每列的兩端,有一些狹縫,光線可以從中射入盒子,也可以射出盒子。
如Hint當中的圖所示,從2號狹縫射進的光線會經過反射而從7號狹縫當中射出。
為了方便起見,我們將第1~n列的左右兩端狹縫編號分別是1~n(左側,由上至下) 以及n+m+1~2*n+m(右側,由下至上)。
Andris想請你設計一個盒子,使得從每個狹縫射入的光線都會由指定的狹縫射出。
你可以假設這樣的盒子一定存在。噢對了,這個問題可能會有很多答案,因此我們需要利用「單向互動函式」回報你的答案~
在程式碼的最上端,請引入 #include "lib1405.h"該標頭檔。
當中只有一個函式:void Report(int flag)。
請依照順序將你構造出來的盒子,由上至下、由左至右的每一格,有無鏡子的狀況利用這個函式回報結果。
如果有鏡子請傳入1,否則傳入0。
Input Format
輸入的第一列為兩個正整數n, m(1<=n,m<=500),代表盒子的列數(row)和行數(column)。
接下來有 2*(n+m)個正整數,第i個數代表從第i個狹縫射入的光線應該從哪一個狹縫射出。
Output Format
本題不需要Output任何東西,請利用Report()函式回報你的答案。
Sample Input 1
9
7
10
8
6
5
2
4
1
3
Sample Output 1
Hints
你可以依序傳入的是:
Report(0);
Report(1);
Report(0);
Report(0);
Report(1);
Report(1);
表示成真正的盒子樣子會變成:
0 1 0
0 1 1

Problem Source
原TIOJ1405 / 快樂暑假營第四次練習比賽。Problem Setter:Tmt。
(Adapted From BOI 2001 Box of Mirrors, 算法藝術 P.1
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 4 |
| 2 | 1 | 4 |
| 3 | 2 | 4 |
| 4 | 3 | 4 |
| 5 | 4 | 4 |
| 6 | 5 | 4 |
| 7 | 6 | 4 |
| 8 | 7 | 4 |
| 9 | 8 | 4 |
| 10 | 9 | 4 |
| 11 | 10 | 4 |
| 12 | 11 | 4 |
| 13 | 12 | 4 |
| 14 | 13 | 4 |
| 15 | 14 | 4 |
| 16 | 15 | 4 |
| 17 | 16 | 4 |
| 18 | 17 | 4 |
| 19 | 18 | 4 |
| 20 | 19 | 4 |
| 21 | 20 | 4 |
| 22 | 21 | 16 |
