1719 測資加強 已 rejudge
1404 . 照亮的山景
TopCoder
Tags
Description
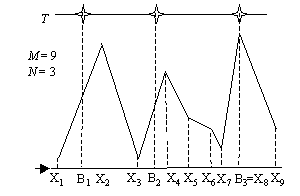
在一片山的上空，高度為T處有N個處於不同水平位置的燈泡，如上圖所示。
如果山的邊界上某一點與第i盞燈的連線不經過任何山稜線上的一點，我們稱第i盞燈可以照亮該點。
請問至少要打開幾盞燈，才能照亮山上每一個轉折點？
Input Format
輸入可能包含多筆測試資料。
對於每筆測試資料：
第1列：一個整數M (1<=M<=100,000)，代表山稜折線的轉折點個數。第2～M+1列：Xi Hi，依序代表轉折點的水平座標以及垂直海拔高度。(-100,000<=Xi, Hi<=100,000)
所有轉折點座標將以X座標由小到大排列。第M+2列：N T，其中N代表燈泡個數，T代表所有燈泡的高度，該高度必定高於整座山最高轉折點的高度。
(1<=N, T<=100,000)第M+3列：有N個整數 B1 B2 ... BN，代表N個燈泡的水平座標，且依座標值由小到大排列。
Output Format
如果可以點亮某幾盞燈而照亮所有轉折點，請輸出最少需要點亮的燈泡數量。
否則請輸出 "you need more bulbs!"(不包含雙引號)。
Sample Input 1
6
1 1
3 3
4 1
7 1
8 3
11 1
4 5
1 5 6 10
6
1 1
3 3
4 1
7 1
8 3
11 1
2 5
1 5
1 1
3 3
4 1
7 1
8 3
11 1
4 5
1 5 6 10
6
1 1
3 3
4 1
7 1
8 3
11 1
2 5
1 5
Sample Output 1
2
you need more bulbs!
you need more bulbs!
Hints
在第一筆範例測試資料中，選擇位置為1以及6的兩個燈泡，即可照亮每個轉折點。
Problem Source
原TIOJ1404 / 快樂暑假第四次練習比賽。Problem Setter：Tmt。
(Adapted From CEOI 2000 Problem 6, 算法藝術P.13)
題目修正by hiiragi4000
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 12 |
| 2 | 1 | 12 |
| 3 | 2 | 12 |
| 4 | 3 | 12 |
| 5 | 4 | 12 |
| 6 | 5 | 12 |
| 7 | 6 | 12 |
| 8 | 7 | 16 |