1343 . [IOI 2007, Day 1] Sails

Submit
Status
Discussion / Solution
Ranklist
Back to Problems List

TopCoder

Caido
$\mathbb{W}\mathcal{aimai}\sim$

User's AC Ratio

92.0% (23/25)

Submission's AC Ratio

66.1% (39/59)

Tags

IOI 2007-IOI

Description

有一艘海盜船正在建造中。這艘船有N根船桅，每根船桅由同等長度的船桅片段所組成。每根船桅的片段數即是該根船桅的高度。每根船桅上各掛置了數片船帆，每一片船帆剛好可以掛在一個船桅片段上。船桅上的船帆可以掛在該船桅上任一船桅片段位置，但是每一船桅片段只能掛一片船帆。

不同的船帆掛置方式，受風時可產生不同的推力。某一船帆前面如有其他的船帆，該船帆受到的風力就會較小，而所能產生的推力也較小。定義每一船帆的反效率(inefficiency)為位於這片船帆後面且同等高度的船帆數。請注意「在前面」或「在後面」是跟船的方向有關，在下圖中，「前面」指的是左邊，「後面」指的是右邊。

整艘船的總反效率則為所有船帆反效率的總和。

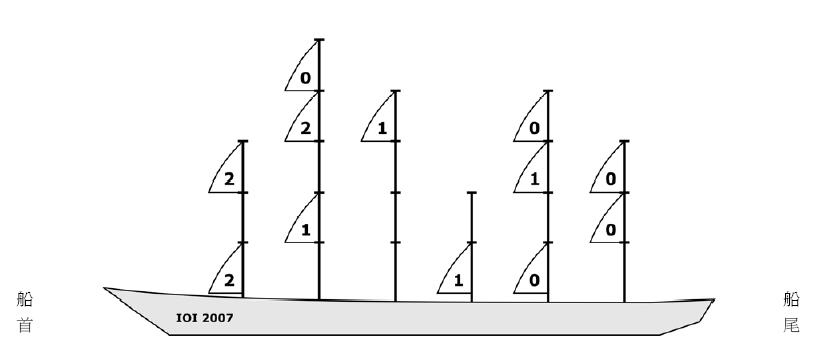
這艘船有6根船桅，從船首（圖中左邊）到船尾每根船桅的高度分別為3, 5, 4, 2, 4, 3。這個船帆配置的方式可產生的總反效率為10。個別船帆的反效率即為圖中船帆內的數字。

請寫一個程式，當給定N個船桅的高度及船帆數時，計算出最小的總反效率。

Input Format

輸入的第一行有一整數N (2 ≤ N ≤ 100 000)，代表這艘船上的船桅數。接下來的N行，每行都有兩個整數，H與K (1 ≤H ≤ 100 000, 1 ≤ K ≤ H)，分別代表每根船桅的高度與船帆數。船桅給定的順序是從船首到船尾。

Output Format

輸出一整數，即這艘船的最小總反效率。 注意：請用64-位元整數運算及輸出結果 (C/C++: 用 long long, Pascal: 用 int64)

Sample Input 1

6
3 2
5 3
4 1
2 1
4 3
3 2

Sample Output 1

10

Hints

Problem Source

原TIOJ1343 / IOI 2007, Day 1 problemsetter: seanwu

Subtasks

No. Testdata Range Score
1 0 5
2 1 5
3 2 5
4 3 5
5 4 5
6 5 5
7 6 5
8 7 5
9 8 5
10 9 5
11 10 5
12 11 5
13 12 5
14 13 5
15 14 5
16 15 5
17 16 5
18 17 5
19 18 5
20 19 5

Testdata and Limits

No. Time Limit (ms) Memory Limit (VSS, KiB) Output Limit (KiB) Subtasks
0 1000 65536 262144 1
1 1000 65536 262144 2
2 1000 65536 262144 3
3 1000 65536 262144 4
4 1000 65536 262144 5
5 1000 65536 262144 6
6 1000 65536 262144 7
7 1000 65536 262144 8
8 1000 65536 262144 9
9 1000 65536 262144 10
10 1000 65536 262144 11
11 1000 65536 262144 12
12 1000 65536 262144 13
13 1000 65536 262144 14
14 1000 65536 262144 15
15 1000 65536 262144 16
16 1000 65536 262144 17
17 1000 65536 262144 18
18 1000 65536 262144 19
19 1000 65536 262144 20
Submit
Back to Top