在魔法世界當中，有一種具有強大法力的道具，稱為「魔術方塊」。

為了不被凡人發現其奧妙，魔法世界和凡人世界的魔術方塊的樣子差不多。然而，魔法世界的魔術方塊實際上是由$N$個大小相等的小立方體組成，並且可以用法術控制每個小立方體的移動。然而，無論怎麼移動，每個小立方體都會有至少一個面完整地貼附在另一個小立方體的某個面之上，並且小立方體的三個相鄰面分別會朝向正東、正北與正上方。

更令人驚訝的是，這些小立方體還有獨特的排列規則。為了完整地解說這個規則，我們引進凡人的座標系統來說明。
假設每一個小立方體的長、寬、高都是一個單位，x, y, z軸分別為東、北、上方，並且所在的位置都在第一卦限（x, y, z座標值皆大於0），那麼這些小立方體的排列必須滿足：如果xy、yz、xz平面都有擋板，且每個小立方體都視為無摩擦力的剛體，並受到朝(-1, -1, -1)方向的重力時，這些小立方體不會因重力而移動。換個方式來說，對於每個小立方體，其西、南、下方都必須是一個別的小立方體或xy、yz、xz平面的其中之一。

以下是一個由9個小立方體所組成的魔術方塊的一種排列方式。

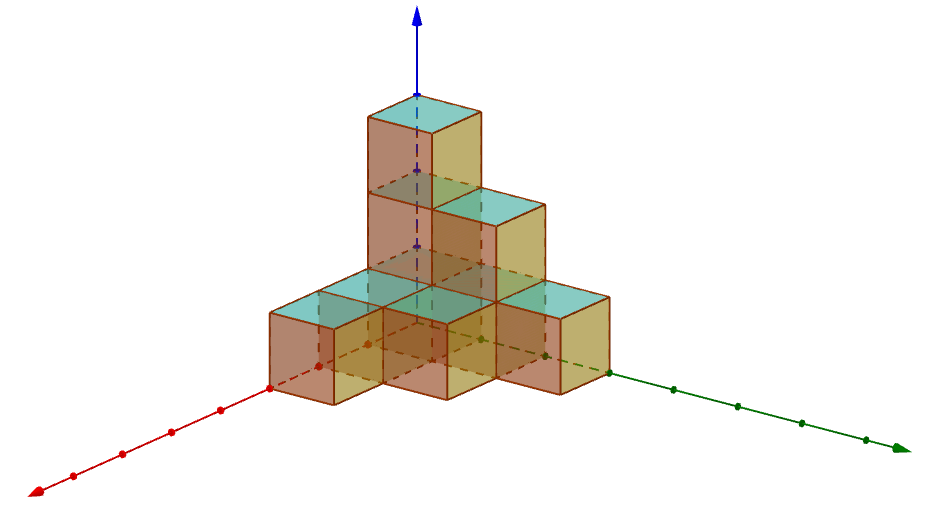
由於其法力強大，這個道具可以進攻、也可以防守。無論當前的魔術方塊排列成甚麼樣子，都可以作為進攻用途；但是只有當魔術方塊只佔據z=0到z=1之間的空間（也就是展開成一個大平臺）時才能作為防守用途。
魔術方塊在不同的排列下，發出進攻或防守的方法都不一樣。愈厲害的魔法師可以駕馭愈多型態的魔術方塊。因此請你計算出，一個由$N$個小立方體組成的魔術方塊，總共有幾種不同的進攻（或防守）方法。

要注意的是，雖然小立方體沒有方向性（也就是不管哪一面朝正北都可以），但是魔術方塊的排列是有方向性的。舉例來說，延伸成南北一長條的魔術方塊和延伸成東西一長條的魔術方塊並不能視為同一種排列。