1273 . [IOI 2012] City 西梯
TopCoder
Description
西梯咖啡最近新開了一個咖啡廳分店,因此他們委派李奧納多進行咖啡廳的擺設。身為專業的空間設計師,李奧納多對於咖啡廳的擺設有獨特的個人見解。
因為西梯咖啡很有錢,他們新開的分店很大,可以視為一個231 * 231 公尺的正方形平面,朝向正北。另外,咖啡廳內也以1*1公尺的正方形地磚鋪地,西北角的地磚定義為(0, 0),東南角的為(231 - 1, 231 - 1)。
顯而易見的,除了邊界的方格以外,任何一個地磚 (i, j) 皆與四個地磚 (i, j + 1), (i, j - 1), (i + 1, j), (i - 1, j) 相鄰。
李奧納多現在有N個1*1公尺的正方形桌子,他負責的就是把這N個桌子擺到咖啡廳內。然而,李奧納多對於桌子的擺設有以下幾個基本要求:
一、每個桌子只能佔據恰好一個地磚。
二、邊界的地磚不能擺桌子。也就是說,當地磚 (i, j) 符合1 ≤ i, j ≤ 231 - 2 時,這個地磚就可以擺桌子;否則就不能擺桌子。
三、任意兩個「沒桌子的地磚」間,都必須存在至少一條不經過任何「有桌子的地磚」的路徑。(當然,這個路徑只能在相鄰的地磚間移動,不能對角移動)
四、任意兩個「有桌子的地磚」間,都必須存在至少一條不經過任何「沒桌子的地磚」的路徑。
例如,下圖四種桌子的擺法都不符合基本要求(黃色代表有桌子的地磚)。左邊數來,前兩個不符合規則三,第三個不符合規則四,最後一個三、四都不符合。
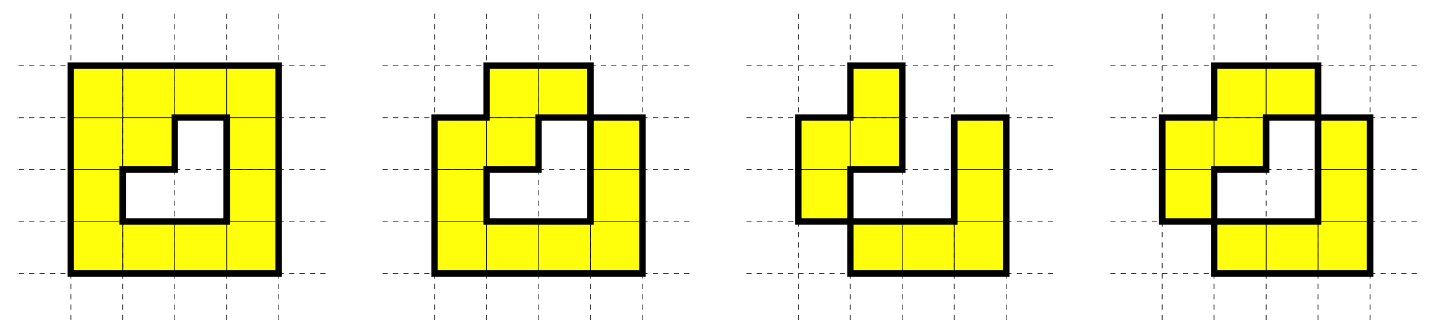
對於每種符合基本要求的桌子擺法,李奧納多定義了「美感指數」來衡量這種擺法的美感。
要了解美感指數,我們先定義兩個桌子之間的「最短路徑長」。
兩個桌子A和B(A≠B)之間的「最短路徑長 d(A, B)」即是,從A出發抵達B,所有不經過任何「沒桌子的地磚」的路徑中最短的一條,經過的桌子數(不計算起點但計算終點)。我們又稱 (A, B) 為一組「桌子對」。
而美感指數的定義即是所有不同的「桌子對」的最短路徑長的總和模1,000,000,000(109 )的結果。假如我們將桌子由 V0 編號到 VN-1 ,我們可將「美感指數」表達成

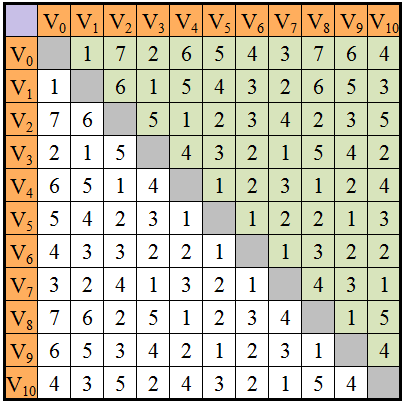
例如對於左上圖的桌子配置,其最短路徑長的表格如右上圖。而美感指數的值便是所有白色底格子中的值相加,等於174。
由於美感指數的計算實在是有點複雜,李奧納多先計畫好很多種符合基本要求的桌子擺放方式。在每一個計畫當中,李奧納多會告訴你每一個桌子所在地磚的座標,而你的任務是告訴他該種桌子擺放方式的美感指數。
Input Format
本題沒有輸入,如果你輸入了任何東西可能會導致各種不可預期的結果(?)。
請#include "lib1273.h"之後實作下列函數。這個函數傳入三個參數,第一個參數是一個整數N,代表桌子的數量;第二、三個參數X、Y都是長度為N的陣列,代表桌子 Vi 在 (X[i], Y[i]) 的地磚上。這個函數要回傳該種桌子擺放方式的美感指數。
int DistanceSum(int, int[], int[]);
如果你的函數名稱不對或者長得不像上面那行,你將會獲得一個CE。
在一次執行當中,這個函數會被呼叫很多次,所以請確保函數中有進行初始化。
對於11%的測資,N ≤ 200。
對於21%的測資,N ≤ 2,000。
對於23%的測資,N ≤ 100,000,並且保證任兩個有桌子且X或Y座標相同的地磚之間,每個地磚都有桌子。
對於所有的測資,N ≤ 100,000。
Output Format
本題沒有輸出,如果你輸出了任何東西,你將會獲得一個WA。
Hints
這裡有一個測試用的標頭檔,可以用來測試。
Problem Source
IOI 2012 Day 2
Judge / Description by Yihda Yol
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 11 |
| 2 | 1 | 21 |
| 3 | 2 | 23 |
| 4 | 3 | 45 |
