1270 . [IOI 2012] Rings 玲思
TopCoder
Description
「玲思」──一種傳說中具有神秘力量的物品,只要將它正確組裝,就能獲得大量的寶藏。
玲思在未組裝前看起來只是一堆圓環,可以拆開、也可以組合。任何一個圓環可以接上任意數量的圓環。
為了瞭解玲思運作的原理,我們先定義圓環組裝的基本結構:圓環鍊。一條圓環鍊定義為n(≥1)個圓環頭尾相接構成的結構。例如下圖便是一個圓環鍊。

很明顯地,在n≥2的情況,除了頭尾的兩個圓環只與另一個圓環相接,其餘所有的圓環都與另外兩個圓環相接。當然,n=1的情況,也就是只有一個圓環,也算是圓環鍊。
當然,玲思沒有那麼容易組裝,因為可以構成各種複雜的結構。然而,有一個人們研究玲思時常用的指標,即「特殊圓環」的數量。
我們知道,如果玲斯上任何一個圓環消失,將導致玲思的結構改變。對於玲思上的每一個圓環,如果那個圓環消失後,剩下的所有的環構成很多個圓環鍊,則稱該圓環為一個「特殊圓環」。
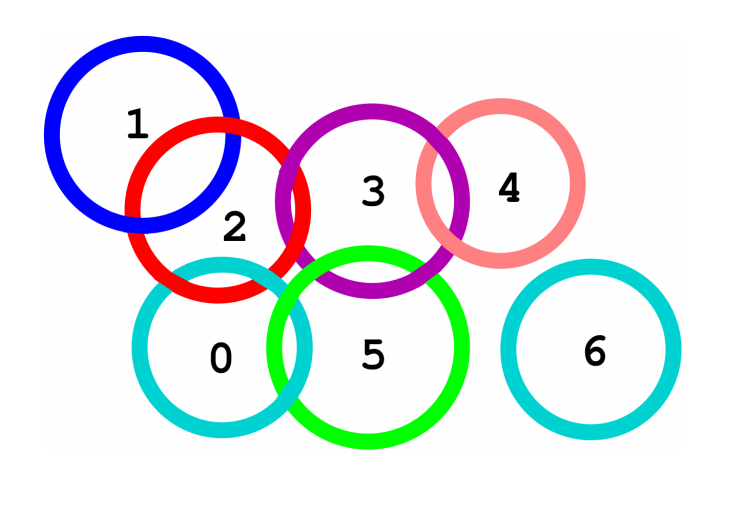
例如上圖,編號2和編號3的圓環都是特殊圓環,然而編號0, 1, 4, 5, 6都不是。
現在,玲思的所有圓環都是分開的。喵喵想要透過把一次一次把兩個環接起來的方式,完成玲思。然而,為了順利完成,他希望能隨時隨地查詢特殊圓環的數量。因此,你的任務就是紀錄他把那些圓環接起來,並隨時應付他的查詢。
Input Format
本題沒有輸入,如果你輸入了任何東西可能會導致各種不可預期的結果(?)。
請#include "lib1270.h"之後實作下列三個函數。如果你的函數名稱不對或者長得不像下面那些行,你將會獲得一個CE。
void Init(int);
void Link(int, int);
int CountCritical();
第一個函數傳入一個值N,代表玲思有幾個環,會在一次組裝的開始呼叫。
第二個函數傳入兩個值A、B,代表喵喵要把A、B兩個環接起來。
第三個函數代表喵喵想要知道特殊圓環的數量,必須回傳對應的答案。
在一次執行當中,喵喵會想要嘗試組裝很多次玲思,所以請確保函數中有進行初始化。
以下敘述以L代表呼叫Link的次數,以P代表呼叫CountCritical的次數。
對於20%的測資,N ≤ 5,000,L ≤ 5,000,P = 1;唯一的一次CountCritical必在所有Link之後呼叫。
對於17%的測資,N ≤ 1,000,000,L ≤ 1,000,000,P = 1;唯一的一次CountCritical必在所有Link之後呼叫。
對於18%的測資,N ≤ 20,000,L ≤ 10,000,P = 100。
對於14%的測資,N ≤ 100,000,L + P ≤ 100,000。
對於所有的測資,N ≤ 1,000,000,L + P ≤ 1,000,000。
Output Format
本題沒有輸出,如果你輸出了任何東西,你將會獲得一個WA。
Hints
這裡有一個測試用的標頭檔,可以用來測試。
Problem Source
IOI 2012 Day 1
Judge / Description by Yihda Yol
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 20 |
| 2 | 1 | 17 |
| 3 | 2 | 18 |
| 4 | 3 | 14 |
| 5 | 4 | 31 |
