1129 . 聚集問題
TopCoder
Description
上體育課時,在操場上通常同班同學會大致聚在一起而形成一個聚集。因此,藉由觀察操場上學生的聚集情形,我們可以大致知道操場中有幾個班級正在上體育課。
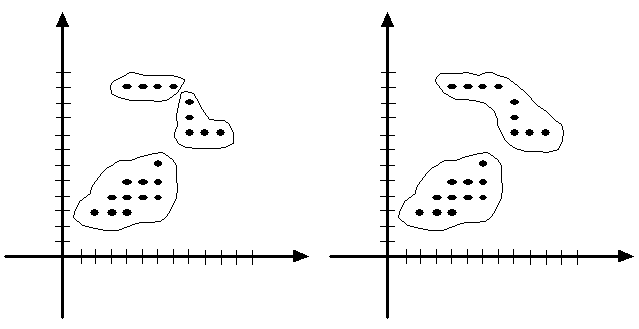
上述學生聚集的判斷,可以藉由電腦來幫忙完成。假設操場的形狀為長方形,我們在操場上定一平面座標,此座標的原點選在操場的一角,而平面座標的兩條軸分別平行於長方形操場的長短兩邊。於是我們可以將操場上的學生,以點的方式表示在座標平面上。我們說一點屬於某一聚集,意思是指此點與在此聚集中至少存在有一點,其相互之間的距離小於等於一個預先給予的門檻值C。以下面左圖為例,若座標平面中每個點的座標值皆為整數,則當給予的聚集門檻值C = 1時,平面中的點會形成3個聚集(如下左圖所示);但若給予的門檻值C = 2時,則只形成2個聚集(如下右圖所示)。
此題中任兩點座標
 之間的距離定義如下:
之間的距離定義如下:
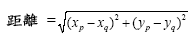
為了避免開根號函數計算可能產生的誤差,你可使用 C2和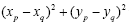 做比較,以決定此兩點p、q之距離是否小於等於門檻值C。
做比較,以決定此兩點p、q之距離是否小於等於門檻值C。
請設計一程式,能夠將一群平面座標上的點依據事先給定的聚集門檻值C加以分群。程式將自動產生一組座標點,其產生方式如下。假設我們要產生B個座標點,第一個座標點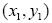 的產生方式為
的產生方式為
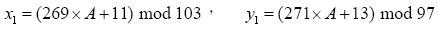
其中A是一個事先給予的種子值,其值為正整數,而x mod y 的意思是指將 x 除以y後的餘數值。在產生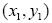 後,接著產生後續的座標點
後,接著產生後續的座標點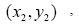
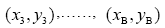 其產生方式如下:
其產生方式如下:
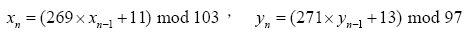
其中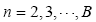 。上述產生點的方式,有可能會有重疊的點,而重疊的點在此視為不同點。
。上述產生點的方式,有可能會有重疊的點,而重疊的點在此視為不同點。
依此敘述所示,則當A=1,B=3,程式將產生3個座標點 (x1, y1) = (74, 90) , (x2, y2) = (38, 56) , (x3, y3) = (36, 57),在 C=2時,會形成3個聚集,而C=3時,只會形成2個聚集。
Input Format
輸入檔可能包含多筆測試資料。每筆測試資料佔一列,包含三個正整數A,B,C。第一個數字A為種子值,1<=A<=100,第二個整數B為所要產生座標點的個數,1<=B<=4000,最後一個整數C為聚集門檻值,1<=C<=1000。
Output Format
對於每筆測試資料請輸出兩列,第一列顯示共有幾個聚集,第二列顯示各個聚集所含點的個數(由小至大排列),並以空白分開。
Sample Input 1
5 25 19 1 1000 7
Sample Output 1
6 1 2 2 4 5 11 8 36 84 89 96 99 166 212 218
Hints
Problem Source
原TIOJ1129 / 94北市賽(prob 5)。Special thanks:kelvin。
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 50 |
| 2 | 1 | 50 |
