數學老師孔智慧帶了小明與阿娟來到了一個遊戲房，房間裡有編號1、2、3、4、5一共5個桶子，每個桶子各裝有不同數目的黑球和白球，而從每個桶子中拿到黑球與白球的機率如下圖所示，例如從編號2號桶中拿到白球的機率為0.8、拿到黑球的機率為0.2。

孔老師將會從這5個桶子中依不同次序拿出若干個黑球或白球的組合，讓小明與阿娟來猜猜有哪一些拿法是最有可能的。孔老師也透露說他每次都會先從編號1號的桶子開始拿第一顆球，當每次拿出一顆球後會再馬上放回原桶子，並且有可能在原桶子或是換到下個桶子中繼續拿出下一顆球，例如當他在編號1號桶中拿出一顆球後，一定會換到編號2號桶繼續拿出下一顆球，而在編號2號桶中拿出一顆球後，有可能繼續留在2號桶或是換到1號、3號或4號桶繼續拿出下一顆球，機率分別是0.4、0.2、0.2、0.2，對於其他桶子可能留在原桶子或者換到別的桶子拿球的機率則如下圖所示。再者，當孔老師說他只拿出一顆球(不論白球或黑球)，則一定是在編號1號桶中拿到；當孔老師拿出球的順序是“白球-白球”、“白球-黑球”、“黑球-白球”、 “黑球-黑球”中的任一組時，則拿球的桶子順序一定是為“1-2”。

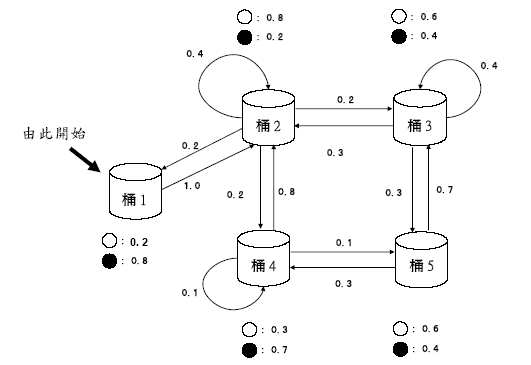
孔老師於是希望小明與阿娟來幫他找出當拿出不同球序列時，可能對應的最佳桶子序列排名前幾名產生球序列的機率和。而桶子序列的排名是先以桶子序列產生球序列機率高低來排名，機率高者排在前面；當兩個桶子序列產生球序列的機率相同時，則再以桶子序列的編號大小來決定排名，是以桶子序列的編號大者排名在前。例如，孔老師拿出球順序是”白球-黑球-黑球”，則可能對應桶子序列共有4種，分別為“1-2-1”(機率為0.0064)、“1-2-2”(機率為0.0032)、“1-2-3”(機率為0.0032)、“1-2-4”(機率為0.0056)。所以桶子序列排名前二名的為“1-2-1”與“1-2-4”(機率和為0.0064+0.0056=0.012)；桶子序列排名前三名的為“1-2-1”、“1-2-4”及“1-2-3”(機率和為0.0064+0.0056+0.0032= 0.0152)；桶子序列排名前四名的為“1-2-1”、“1-2-4”、“1-2-3”及“1-2-2” (機率和為0.0064+0.0056+0.0032+0.0032 =0.0184)。聰明的你(妳)請來幫小明與阿娟來回答這個問題。

Constraints

已知孔老師最多只會拿出15顆球。