某學校有一片狹長形狀的畸零地，其寬度、長度分別為30公分及n×10公分(其中 n 為輸入之值，n為奇數，n>=3)，但在西北角缺了寬度、長度均為10公分的一角。現在我們要使用 (3×n-1)/2 塊磁磚將此片畸零地鋪滿，每塊磁磚的寬度、長度均為10公分及20公分，我們想知道共有多少種鋪法。請你撰寫一個程式來求出答案。以下圖為例，當 n=3 時，可看出共有4種不同的鋪法。

當n=5時，由下圖，可看出共有15種不同的鋪法。

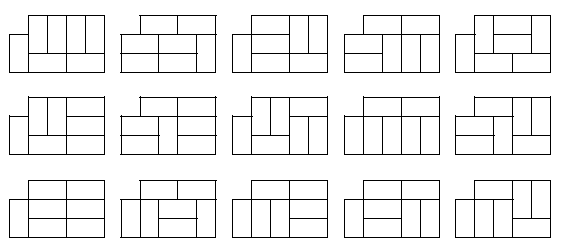
Constraints

n為奇數，3<=n<=41。