分子運動是物理學中一個無法用肉眼觀察但卻可以用數學分析的有趣問題。

　　本題假設有一個分子，m，被放在一個正方形的框子中，只以二維平面的方向移動。給定分子有一個初始運動速度為6 公分/每秒，即使在碰到框子的邊緣反射後，分子的運動速度都不會改變。其中分子的大小與重量我們忽略不考慮。當分子碰到框子的邊緣時會依入射時的相同角度反射出去，並且繼續以6 公分/每秒的速度移動，如下圖所示。

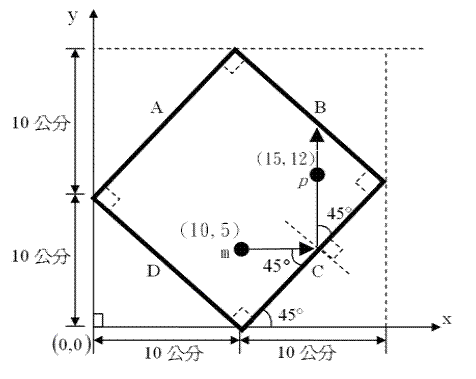
　　假設正方形框子以上圖的方式放在二維平面座標系中，框子的四個邊分別稱之為A、B、C、D，而這四個邊的厚度我們忽略不考慮。其中C 邊與水平座標x 軸成 45度夾角(角度單位：度)，因此框子的每一邊長均為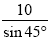公分。其中C 邊與D 邊的交點為(10,0)。一開始時，分子m 的座標(x,y) 為(10,5) (座標長度單位：公分)；運動速度為6 公分/每秒；在第0 秒時的行進方向為往右，與水平座標x軸平行。請問在第t 秒時，分子m 所在的座標為何?

　　舉例來說：當輸入t = 2 時，輸出結果為圖中p點的座標(15,12)。

Constraints

• t是一個介於0至20000之間的整數。


• 在任意時間中，分子m的座標(x,y)一定落在正方形框子內。