二進位數在計算機科學的領域中有莫大的應用，然而最早二進位數的概念是哪裡的人想出來的呢？答案是中國人。

　　現代二進位制四則運算器的發明人萊布尼茲曾說：「我的這種不可思議的新發明，……是因為我發現了一位聖人的古代文字的秘密，這位古代聖人，就是 3000 多年前，中早期的君王伏羲氏。」

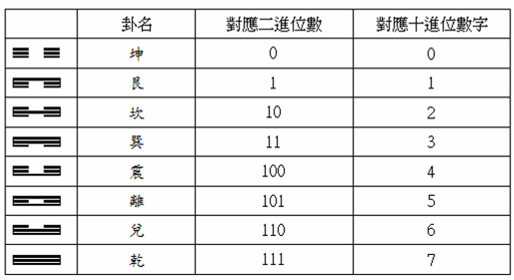
　　事實上萊布尼茲所指的就是易經中的八卦，如表所示，揭示了十進位和二進位數字的對應法。易經中則一條長型的直線為「陽爻」，中間有斷的稱作「陰爻」，故有以陰陽二氣生四象八卦之稱。現在注意到八卦中下面四個卦震、離、兌、乾；其中離、兌、乾這三個卦的陽爻數多於陰爻，我們稱它們所對應的數 $5, 6, 7$ 為「陽數」，對一個自然數 $N$ 來說，它是否為「陽數」的定義就是將 $N$ 轉換成二進位，若 $1$ 的個數多於 $0$ 的個數(不包含等於)，則稱 $N$ 是「陽數」。在八卦之中，艮卦和巽卦亦是陽數。

　　而現在我們想解決的問題是，已知一個自然數 $M$，則在 $1\sim M$ 的範圍中，一共有多少個陽數呢。請你撰寫一個程式來解決這個問題。

　　(補充：正如十進位數中我們要求正整數的第一位必不為 $0$，因此我們一個數字 $34$ 不會被寫成 $034$，這裡我們同樣規定二進位正整數中第一位必不為 $0$)