1719 測資加強 已 rejudge
1040 . C.連分數
TopCoder
Description
連分數有許多不為人知的應用，一開始一位印度數學家利用連分數解出了 ax+by=c的一次不定方程式，連分數還跟我們日常生活中的曆法有密切的關係，那什麼是連分數呢？
連分數一般如下面形式：
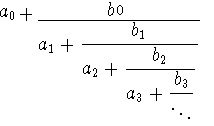
連分數有四種，一種是無窮連分數可以一直延展下去，一種是有窮連分數，而連分數又可分為簡單連分數，即分子部份永遠是 1 ，另一種是非簡單連分數，分子部份是由其他數字所組成。每一個有理數都可以用簡單有窮連分數來表示：
簡單有窮連分數不會一直延展下去，當子分數的分母為一整數時，就要停止。
現在輸入P和Q，請你幫忙將P/Q化為連分數吧。
Input Format
輸入檔第一行有一個數字N代表有幾組測試資料，接下來N行，每行會有兩個數字分別代表 P 和 Q (0 ≤ P,Q ≤ 2147483647 且 Q ≠ 0)。
Output Format
每組測試資料輸出一行，輸出為下面格式：
P/Q = a+1/{b+1/{c+1/{d+...}}}其中a是非負整數，b,c,d,...都是正整數。
Sample Input 1
3
103 24
21 73
4 2
103 24
21 73
4 2
Sample Output 1
103/24 = 4+1/{3+1/{2+1/3}}
21/73 = 0+1/{3+1/{2+1/10}}
4/2 = 2
21/73 = 0+1/{3+1/{2+1/10}}
4/2 = 2
Hints
※2007/10/07:題目敘述修正，感謝seanwu和akira兩位大大。
Problem Source
原TIOJ1040 / NPSC2003初賽(prob C)
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 100 |