[03/31 16:49] 如果你發現你的 Submission 頁面的測資最右側有向下箭頭的符號,可以點開看看裡面有什麼東西 :)
[04/01 12:00] 開板!
[04/01 13:26] pA special judge 部分訊息微調(不影響分數與做題,故不 rejudge)。
[04/01 15:30] 倒數半個小時,大家加油 (?
2355 . 經典題
Description
這次 April Fools Contest 的出題者們很懶。因為他們實在是懶得出題,所以他們決定丟一題裸經典題給你。
你現在有一個序列 $a_0,a_1,\cdots,a_{N-1}$,每個都是不超過 $256$ 的正整數。你想要把這個序列傳給另外一個程式讓它也能得到同樣的序列,但是邪惡的 special judge 會在你傳送的序列中挑選 10% 的數字,然後把它們替換成任意不超過 $256$ 的正整數。
因此,請你寫一個程式把序列 $a_i$ 轉換成 $b_0,b_1,\cdots,b_{M-1}$($1\leq b_i\leq 256$),以及把 $c_0,c_1,\cdots,c_{M-1}$ 轉換回原本的序列 $a_i$,其中 $c_i$ 是把 $b_i$ 中 $\lceil M/10\rceil$ 個數字替換成任意不超過 $256$ 的正整數後所產生的序列。
Input Format
此程式對於每個 subtask 將會被執行兩次,兩次執行的 argv[1] 依序會是 0、1。
第一次執行時,輸入的第一行是一個正整數 $T$,代表測資筆數。接下來的 $T$ 行每行為一筆測資,包含 $N+1$ 個以空白隔開的正整數 $N,a_0,a_1,\cdots,a_{N-1}$,意義如題目所述。
第二次執行時,輸入的第一行是一個正整數 $T$,代表測資筆數。接下來的 $T$ 行每行為一筆測資,包含 $M+1$ 個以空白隔開的正整數 $M,c_0,c_1,\cdots,c_{M-1}$,意義如題目所述。
對於所有的測資,$64\leq N<128$。
保證 special judge 替換數字的方式是固定的:對於每一筆測資,同樣的 $b_i$ 會得到同樣的 $c_i$。(但是同樣的 $b_i$ 在兩筆不同的測資中可能會得到不同的 $c_i$。)
Output Format
第一次執行時,請對每筆測資輸出一行包含 $M+1$ 個以空白隔開的正整數 $M,b_0,b_1,\cdots,b_{M-1}$,意義如題目所述。
第二次執行時,請對每筆測資輸出一行包含 $N+1$ 個以空白隔開的正整數 $N,a_0,a_1,\cdots,a_{N-1}$,代表原本的序列。
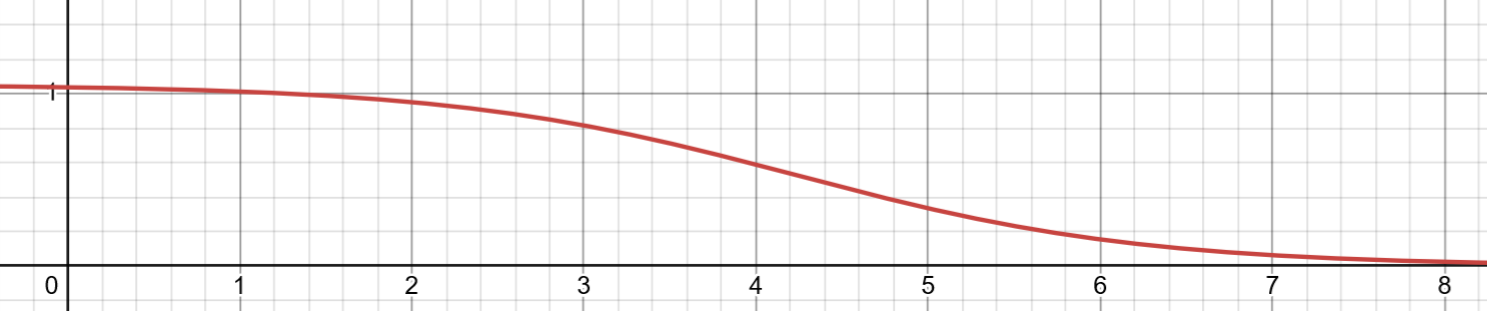
在所有測資都輸出正確的前提下,每筆測資的分數是 $\frac{20}{15e^ {M/N-4}+19}\times X$,其中 $X$ 是該 subtask 的標示總分,而最終該 subtask 的總分則是該 subtask 中所有測資分數的平均。
以下是 $y=\frac{20}{15e^ {x-4}+19}$ 的圖形:
Sample Input 1
1
69 27 252 120 77 190 66 221 234 51 255 245 28 114 176 68 68 251 17 184 98 233 184 190 24 54 86 46 213 113 35 108 226 204 63 148 128 89 83 217 248 198 139 60 156 28 13 39 186 47 229 49 110 78 110 232 129 213 229 151 177 237 243 54 202 245 209 153 138 95
# 第二次執行(替換的數字僅供參考,不代表真實情況)
1
10 1 2 3 20 5 6 7 8 9 10
Sample Output 1
10 1 2 3 4 5 6 7 8 9 10
# 第二次執行
69 27 252 120 77 190 66 221 234 51 255 245 28 114 176 68 68 251 17 184 98 233 184 190 24 54 86 46 213 113 35 108 226 204 63 148 128 89 83 217 248 198 139 60 156 28 13 39 186 47 229 49 110 78 110 232 129 213 229 151 177 237 243 54 202 245 209 153 138 95
Hints
出題者很懶所以不想給 Hint。
Problem Source
TIOJ April Fools Day Contest 2024 pE
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0 | $T=1$(範例測資) | 1 |
| 2 | 1 | $T=1500$ | 99 |