1719 測資加強 已 rejudge
1484 . 仙人掌
TopCoder
Tags
Description

一個有向圖是由點集 V 以及邊集 E ∈ {V x V} 所組成。
一條有向邊(u,v)代表有一條由 u 指向 v 的邊(而(v,u)則是反方向)。
而一個有向圈則是由有向圖中的邊集:(u1, v1), (u2, v2),…, (uk, vk),所組成,並且ui+1 = vi for i = 1, …, k-1, u1=vk.
如果有向圈不重複經過同一頂點即可達成圈的特性,我們則稱其為簡單圈。
強連通圖則是指有向圖內的任兩點皆可找到路徑達到彼此。
現在我們發明出了一種性質『仙人掌』性質:當一個圖屬於強連通圖 且 每條邊都恰屬於一個簡單圈 時,我們稱其具有『仙人掌』性質。
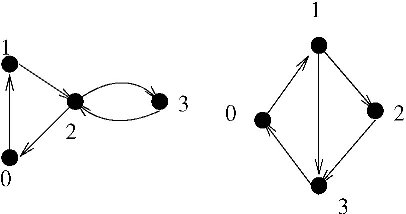
在上圖中,左邊的圖很明顯符合『仙人掌』性質,但在右邊的圖中,(0,1)這條邊被兩條簡單圈所包含,所以他不屬於『仙人掌』性質。
現在給你很多圖,你能判斷他們哪些屬於『仙人掌』性質嗎?
Input Format
本題有多筆測試資料:
第一行有一個數字T,代表接下來有 T 個圖需要判斷。
每筆資料的:
第一行有一個數字 n ,代表圖中有 n 個點。 ( n <=105)
第二行有一個數字 m ,代表圖中有 m 條邊。
接下來有 m 行,每行有兩個數字a,b,代表存在一條(a,b)的有向邊
Output Format
對於每筆測試資料輸出是否符合『仙人掌』性質。
若符合請輸出"YES"(不含雙引號)
若不符合請輸出"NO"(不含雙引號)
Sample Input 1
2
4
5
0 1
1 2
2 0
2 3
3 2
4
5
0 1
1 2
2 3
3 0
1 3
4
5
0 1
1 2
2 0
2 3
3 2
4
5
0 1
1 2
2 3
3 0
1 3
Sample Output 1
YES
NO
NO
Hints
Problem Source
原TIOJ1484 / 建中校內培訓第六次模擬考試。
Problem Setter:hallogameboy、peter50216
(Adapt From:Uva OJ)
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 10 |
| 2 | 1 | 10 |
| 3 | 2 | 10 |
| 4 | 3 | 10 |
| 5 | 4 | 10 |
| 6 | 5 | 10 |
| 7 | 6 | 10 |
| 8 | 7 | 10 |
| 9 | 8 | 10 |
| 10 | 9 | 10 |
